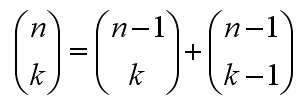

Binomialkoeffizient berechnen |
Auf dieser Seite können Sie sich den Binomialkoeffizienten "n über k" berechnen lassen.
Was das ist, zu welchem Zweck diese Seite entstanden ist usw., wird in der Beschreibung unten näher erläutert.
Die Berechnung geschieht auf drei verschiedene Arten: Einmal mit Hilfe der Fakultätsfunktion, einmal als rekursiv aufgerufene Summe und einmal mit Hilfe des Pascalschen Dreiecks.
Für jeden Rechenweg wird die benötigte Rechenzeit ausgegeben.
Auch zu den Rechenwegen gibt es in der Beschreibung unten detailliertere Informationen.
Geben Sie die Werte für n und k ein, wählen Sie die Kontrollkästchen unter den Rechenmethoden, die Sie benutzen möchten, und klicken Sie auf das Gleichheitszeichen.
Wenn Sie die Berechnung mittels des Pascalschen Dreiecks durchgeführt haben, können Sie mit den Plus- und Minus-Tasten den Wert für k um 1 erhöhen bzw. erniedrigen und so diese Binomialkoeffizienten, die nach der Pascal-Methode schon mitberechnet sind, abfragen, ohne dass dafür die Berechnung erneut gestartet werden muss. (Die anderen Ergebnisfelder werden in diesem Fall gelöscht.)
Der Binomialkoeffizient "n über k" ist wie folgt definiert:
| ( | n | ) | := | n! |
| k | k! (n-k)! |
Der !-Operator heißt Fakultät und bedeutet das Produkt aller Zahlen von 1 bis einschließlich des Operanden. Also zum Beispiel:
4! = 1 x 2 x 3 x 4 = 24
Der Fakultätswert von Null ist auf Eins festgelegt:
0! := 1
Seinen Namen trägt der Binomialkoeffizient, weil die Potenzen eines Binoms beim Ausmultiplizieren diese Koeffizienten ergeben, die bei den Potenzkombinationen der beiden Größen in der Klammer stehen.
Beispiel:
(a+b)2 = a2 + 2ab + b2
(a+b)3 = a3 + 3a2b + 3ab2 + b3
(a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
| (a+b)n = ( | n | )an + ( | n | )an-1b1 + ( | n | )an-2b2 + .... + ( | n | )a2bn-2 + ( | n | )a1bn-1 + ( | n | )bn |
| 0 | 1 | 2 | n-2 | n-1 | n |
Neben dieser Funktion spielen die Binomialkoeffizienten in der Kombinatorik eine Rolle:
Wenn man aus einem Behälter mit n nummerierten Kugeln k zufällig herausnimmt, ist die Anzahl der möglichen Kombinationen (ohne Berücksichtigung der Reihenfolge) n über k.
Beim Lotto "6 aus 49" ist die Chance, sechs Richtige zu tippen also
| ( | 49 | ) | = | 13.983.816 |
| 6 |
Außer mit Hilfe des Fakultätsoperators lassen sich die Binomialkoeffizienten auch mit Hilfe des Pascalschen Dreiecks bestimmen:
| 1 | ||||||||||
| 1 | 1 | |||||||||
| 1 | 2 | 1 | ||||||||
| 1 | 3 | 3 | 1 | |||||||
| 1 | 4 | 6 | 4 | 1 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||
| usw. | ||||||||||
Dabei ergeben sich die Koeffizienten einer Zeile als Summe der beiden jeweils darüber stehenden Koeffizienten.
In der Formeldarstellung für den Binomialkoeffizienten liest sich das so:
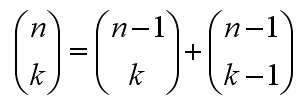
|
Rechnerischer Beweis:
Erweitern beider Summanden mit n, um im Zähler auf das gewünschte n! zu kommen.
Um die beiden Brüche gleichnamig zu machen (Hauptnenner) wird der linke mit (n-k) erweitert.
Nun wird noch der Zähler zusammengefasst ...
... und mit n gekürzt ...
... und wir erhalten die Definitionsformel für den Binomialkoeffizienten n über k. |
Man kann diesen Zusammenhang dazu benutzen, den Binomialkoeffizienten rekursiv berechnen zu lassen: Das Programm berechnet den Binoialkoeffizienten als Summe der beiden kleineren Binomialkoeffizienten, die wiederum so lange mit dem selben Programm berechnet werden, bis k=0 oder n=k ist, man also an den Kanten des Pascalschen Dreiecks angestoßen ist. Das Programm ruft sich bis dahin immer wieder selbst auf.
Um n über k direkt im Pascalschen Dreieck zu bestimmen, nimmt man in Zeile (n+1) des Dreiecks den (k+1)ten Wert, weil die erste Zeile bzw. Spalte der Koeffizient für n=0 bzw. k=0 ist.
"4 über 2" ist also beispielsweise der dritte Wert in der fünften Zeile, also 6.
| ( | n | ) = ( | n | ) = 1 |
| 0 | n |
Diese Formel zeigt sich in den Kanten des Pascalschen Dreiecks, auf denen nur Einsen stehen.
| ( | n | ) = ( | n | ) |
| k | n-k |
Im Pascalschen Dreieck bedeutet diese Formel Symmetrie: Die Zahlen in der linken Hälfte sind die gleichen wie in der rechten.
Das Pascalsche Dreieck selbst hat auch noch jede Menge faszinierender Eigenschaften - z.B. ergeben sich sehr schöne Muster, wenn man die Teilbarkeit der Koeffizienten untersucht - diese sollen aber hier nicht Thema sein.
Dazu gibt es z.B. hier eine schöne Seite.
Sinn und Zweck dieses Programms zur Berechnung des Binomialkoeffizenten sollte ein Vergleich der drei Berechnungsverfahren hinsichtlich Genauigkeit, Rechenaufwand und eventuell Speicherplatzbedarf sein.
Daher die drei Ausgabefelder (in denen ja fast immer die selben Ergebnisse stehen) und die Ausgabe der Rechenzeiten.
Dieses Vorgehen ist nur so lange problemlos, wie das Zwischenergebnis für n! noch einen im Integer-Format darstellbaren Wert hat; andernfalls entstehen Rundungsfehler.
Diese stellen sich so dar, dass entweder eine Fließkommazahl für den Binomialkoeffizienten ausgegeben wird, der aber natürlich immer eine natürliche Zahl ist, oder es entstehen auch ganzzahlige, absolut gesehen sehr große Fehler.
Beispielsweise wird "100 über 20" mit einem Fehler von 100.000 berechnet - der relativ gesehen allerdings nur 2*10-16ausmacht, was aber unter Umständen trotzdem unerwünscht sein kann.
Das größte Argument der Fakultät-Funktion, das noch ein im Integerformat darstellbares Ergebnis liefert ist
n = 21
21! = 51.090.942.171.709.440.000
Überschreitet die Eingabe für n diesen Wert, wird eine Warnmeldung ausgegeben, die auf die Möglichkeit von Rundungsfehlern aufmerksam macht.
Das größte Argument der Fakultätsfunktion, das ein überhaupt noch an einem herkömmlichen Computer mittels Exponentialschreibweise darstellbares Ergebnis liefert ist
n = 170
170! = 7.257415615307994 x 10^306
Wird auch dieser Wert überschritten, erscheint eine entsprechende Information und das Programm schaltet das Berechnungsverfahren mittels Fakultätsfunktion ab.
Die Binomialkoeffizienten sind immer deutlich kleiner als die Fakultätswerte von n; das liegt an der Division in der Definition.
Das bedeutet, dass ein herkömmlicher Rechner durchaus Binomialkoeffizienten für Werte von n und k darstellen kann, deren Fakultäten sein Zahlenformat selbst in der Exponentialschreibweise sprengen.
Um diese Möglichkeit zu erschließen, ist die iterative Berechnung mit Hilfe des Pascalschen Dreiecks erforderlich.
In der hier implementierten Version wird die Eigenschaft des Binomialkoeffizienten ausgenutzt, dass
| ( | n | ) | = | ( | n | ) |
| k | (n-k) |
Im Pascalschen Dreieck spiegelt sich diese Formel in der Symmetrie zur Mittelsenkrechten wieder.
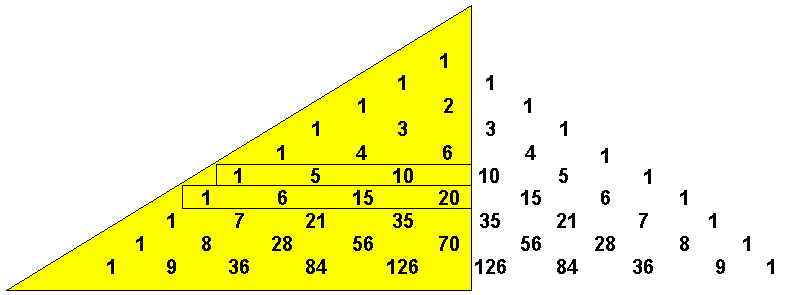
Zur Berechnung wird also der kleinere der Werte k oder (n-k) herangezogen, so dass nur eine Hälfte des Dreiecks berechnet werden muss.
Gespeichert wird jeweils nur die gerade berechnete und die dafür erforderliche vorhergehende Zeile des Dreiecks.
In nachfolgendem Bild ist das veranschaulicht: Berechnet werden nur die Koeffizienten im farblich hinterlegten Teil und zwar Zeile für Zeile - angedeutet durch die beiden Rahmen.
Beim dritten untersuchten Verfahren wird der Binomialkoeffizient rekursiv bestimmt, d.h. die Prozedur ruft sich so lange immer wieder mit n-1 auf, bis die Ränder des Dreiecks erreicht sind. Pro Koeffizient sind dies zwei Aufrufe, einer für k und einer für k-1 (vgl. obige Formel!)
Der Vorteil dieses Verfahrens liegt in der einfachen Programmierung und darin, dass keine Multiplikationsoperationen erforderlich sind, sondern nur Additionen. Nachteilig ist, dass die selben Koeffizienten mehrfach berechnet werden, weil ja jeder zu zwei Koeffizienten der nächsten Zeile beiträgt.
Ob Vor- oder Nachteile überwiegen? Lesen Sie im nächsten Abschnitt!.
Es zeigt sich, dass die Berechnung mittels Fakultätsfunktion immer schneller ist als diejenige über das Pascalsche Dreieck. Selbst bei größtmöglichen Werten für n und k bleibt die Anzeige der Rechenzeit auf Null, d.h. es ist weniger als eine Millisekunde. (Das Funktionieren der Zeitberechnung habe ich überprüft, in dem ich in die Fakultätsfunktion einen alert-Befehl eingebaut habe, so dass die Berechnung so lange unterbrochen ist, bis der Benutzer auf "OK" geklickt hat.)
Dieser Zeitunterschied leuchtet sofort ein, wenn man sich klar macht, wie die Anzahl der Rechenvorgänge von n abhängt:
Bei der Fakultätsfunktion steigt die Zahl der Operationen linear mit der Größe des Arguments: Für 4! werden vier Multiplikationen ausgeführt, für 12! zwölf usw.
Es werden drei Aufrufe dieser Funktion benötigt.
tFakultät ~ n
Beim Pascalschen Dreieck wird zwar nur addiert statt multipliziert (wahrscheinlich dauert eine Addition nicht ganz so lange wie eine Multiplikation), dafür ist die Anzahl der erforderlichen Operationen n x n/2 / 2 (Anzahl Zeilen (n) mal Anzahl Spalten (n/2) des halben Dreiecks, geteilt durch zwei, weil es nur ein Dreieck und kein Rechteck ist.)
Die Rechenzeit hängt also quadratisch von n ab!
tPascal ~ n2
Im Experiment hat sich dieser Zusammenhang sehr schön bestätigt:
"2.500 über 1" zu berechnen, hat auf meinem Laptop 16 Sekunden gedauert, also 6,4msec pro Zeile des Dreiecks.
Für ein doppelt so großes n dauert die Berechnung vier mal so lange: "5.000 über 1" zu berechnen, hat auf meinem Laptop 67 Sekunden gedauert, also 13,4msec pro Zeile des Dreiecks.
Ein vier mal so großer Wert führt zu einer sechzehnfachen Rechenzeit: "10.000 über 1" hat 272 Sekunden gedauert, also 27,2msec pro Zeile des Dreiecks.
(Das Ganze funktioniert auch mit anderen Werten für n und ist unabhängig von k. Probieren Sie es aus!)
Eine Verdopplung von n hat also zu einer Vervierfachung der Rechenzeit bzw. einer Verdopplung der für eine Dreieckszeile benötigten Zeit geführt.
(Die leichten Abweichungen von der Theorie können unter anderem darauf zurückgeführt werden, dass der Internetexplorer das Skript immer wieder unterbricht, um zu fragen, ob es abgebrochen werden soll, weil es so lange läuft.)
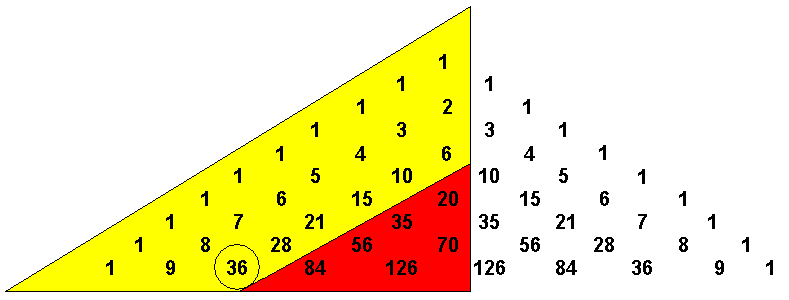
Der implementierte Algorithmus ließe sich hinsichtlich Rechenzeit noch optimieren, wenn man die Größe k bei der Berechnung berücksichtigt:
Man braucht ja nicht das gesamte (halbe) Dreieck berechnen, sondern nur diejenigen Koeffizienten, die zur Berechnung des gewünschten Koeffizienten erforderlich sind; ab der Zeile mit der Nummer 2*k kann man deshalb statt für jede zweite neue Zeile einen Koeffizienten mehr zu berechnen, einen weniger berechnen; der rechte Winkel des halben Pascalschen Dreiecks wird dabei also quasi abgeschnitten.
Das nachfolgende Bild erläutert das am Beispiel "9 über 2": Das Ergebnis ist eingekreist; der rot hinterlegte Bereich braucht nicht berechnet werden.
Allerdings bringt dieses Verfahren nur für kleine k (im Verhältnis zu n) eine Reduzierung des Rechenaufwands.
tPascal,2 ~ n * k | k <= n
Die Tatsache, dass das Pascal-Verfahren eine so große Rechenzeit hat, birgt auf der anderen Seite auch einen Benefit: Im Gegensatz zum Fakultätsverfahren steht am Ende der Rechnung nicht nur ein Koeffizient als Ergebnis zur Verfügung sondern eine gesamte Zeile des Pascalschen Dreiecks.
Um diesen Vorteil nutzen zu können, wurden die Schaltflächen "+" und "-" eingeführt, mit denen nach der ersten Berechnung k inkrementiert bzw. dekrementiert werden kann, wobei nicht komplett neu gerechnet sondern nur der gespeicherte Koeffizient abgefragt wird.
Die rekursive Addition schießt in Sachen Rechenzeit den Vogel ab: Obwohl der Algorithmus mit wenigen Zeilen programmiert ist und obwohl nur addiert werden muss, ist diese Variante mit großem Abstand die langsamste! Woran liegt das?
Wenn man sich genauer ansieht, welche Binomialkoeffizienten jeweils berechnet werden müssen, stellt man fest, dass fast alle mehrfach berechnet werden. Erschreckend ist aber wie viele Funktionsaufrufe zur Berechnung eines Binomialkoeffizienten nötig sind, es ist nämlich der doppelte Wert dieses Koeffizienten minus eins!
| Anzahl Funktionsaufrufe = 2 | ( | n | ) | - 1 |
| k |
Der Beweis für diese Aussage lässt sich hier unter Nr. 4 nachlesen. Außerdem habe ich das in der Testphase des Programms mit einem Zähler verifiziert, der zur Laufzeit die Programmaufrufe mitgezählt hat.
Der relative Fehler ist auch bei der Berechnung mit Hilfe der Fakultätswerte sehr klein; allerdings kann der absolute Fehler bei großen Werten für n sehr groß sein.
In Sachen Genauigkeit ist also das Verfahren mit Pascalschem Dreieck überlegen, ebenso wie die rekursive Addition, die ja auch nur die Addition der kleineren Binomialkoeffizienten zum Ergebnis kommt. Es muss jedoch beachtet werden, dass auch dabei Rundungsfehler auftreten können, wenn die Binomialkoeffizienten selbst nicht mehr in das Integer-Format passen.
Es hat sich gezeigt, dass auch für große n das Hauptproblem die Rechenzeit und nicht der Speicherbedarf ist.
Selbst bei der rekursiven Addition, bei der ja alle Variablen jeder einzelnen Berechnungsroutine - und das können Hunderttausende sein, wie wir gesehen haben - so lange zwischengespeichert werden müssen, bis die Rekursion abgearbeitet ist.
Wenn man die Methode mit Pascalschem Dreieck bezüglich Speicherplatz trotzdem optimieren möchte, kann man zum einen die unter Rechenzeit bereits angesprochene Verbesserung nutzen, die auch die Anzahl der benötigten Array-Elemente von (n+1) auf 2*k reduziert. Zum anderen kann man zwei Arrayelemente einsparen, wenn man die Tatsache ausnutzt, dass sowohl die Werte an der Kante des Pascalschen Dreiecks (alle Eins) als auch jedes zweite Element einer Zeile, das immer gleich der Zeilennummer ist, bekannt sind. Allerdings ist der dadurch bedingte Programmieraufwand im Verhältnis zum Nutzen unangemessen.
Nachfolgendes Bild zeigt den Bereich, der eigentlich nur berechnet werden muss, in orange:
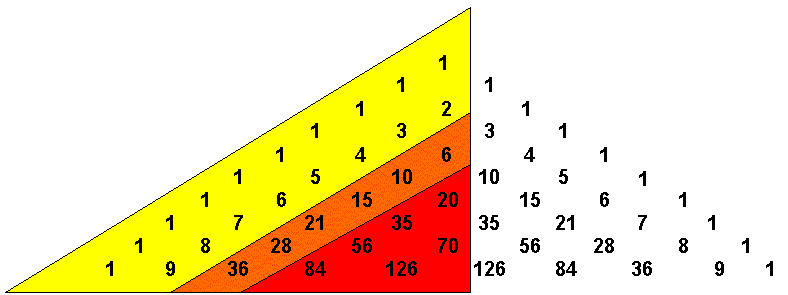
Es gibt eine Formel, die die meisten Nachteile der bisher beschriebenen Berechnungsverfahren vermeidet. Laut Wikipedia ist dies ein im streng-mathematischen Sinn effizientes Verfahren.
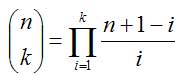
Und nun viel Spaß beim Experimentieren!