Man kann sich mit relativ einfachen Voraussetzungen überlegen, wie sich das Volumen einer Pyramide und eines Kegels berechnet:

Beginnen wir mit der Pyramide: Zunächst sind wir bescheiden und begnügen uns mit einer Näherung: Wir stellen uns die Pyramide nicht als eine ägyptische mit glatten schrägen Wänden sondern als eine mexikanische Pyramide vor, bei der die Wände treppenförmig sind. Die Pyramide besteht also quasi aus Scheiben mit senkrechten Wänden.

Das Volumen jeder dieser Scheiben lässt sich sehr einfach berechnen, es ist nämlich

V_Scheibe = Grundfläche · Höhe

Das Volumen der gesamten Pyramide ist die Summe der Volumina aller Scheiben.

Schon an dieser Stelle, an der ich nur das Konzept beschrieben habe, lässt sich erkennen, dass die Volumenformel, die wir suchen, nicht nur für Pyramiden gilt sondern auch für Kegel und alle anderen Körper mit einer Grundfläche und im Schnitt geraden Mantelflächen, die sich in einer Spitze treffen, denn obige Formel spricht nur von einer Grundfläche der Scheiben - unabhängig davon, wie diese Grundfläche geformt ist. Es kann sich um ein Dreieck (Pyramide), ein Viereck (Pyramide), einen Kreis (Kegel) oder jede andere Fläche handeln.

Nachfolgendes Bild zeigt den Querschnitt durch einen solchen Körper und die Stufen, mit denen wir das Volumen annähern wollen. Gehen wir mal davon aus, dass es sich bei dem Körper um einen Kegel handelt, die Grundfläche also ein Kreis ist. Mit den Schiebereglern lassen sich der Radius R der Kegelgrundfläche, die Höhe H des Kegels sowie die Anzahl der Stufen n einstellen.

Die Grundfläche einer dieser Scheiben beträgt:

A_i = π r_i²

Den Index i habe ich hier nur eingeführt, um die Scheiben auseinanderhalten zu können, denn sie sind natürlich alle unterschiedlich groß. Der Index i ist also gewissermaßen die Nummer der Scheibe.

Nachdem die Idee, wie wir vorgehen wollen, nun klar ist, ist der erste wichtige Schritt, die Größen der einzelnen Scheiben auszurechnen. Nehmen wir an, die Höhe des Kegels H und der Radius seiner Grundfläche R seien gegeben. Ferner können wir uns die Anzahl n der Scheiben, die wir betrachten wollen, zunächst selbst aussuchen.

Wie dick sind die Scheiben?

Das ist einfach zu beantworten: Wir machen die Scheiben alle gleich dick, also hat jede von ihnen die Höhe H/n also die Höhe des Kegels geteilt durch die Anzahl Scheiben.

Wie groß ist der Radius der Scheiben?

Auch das ist nicht so schwer: Auch die Stufen sind in obigem Bild alle gleich groß, was daran liegt, dass der Mantel des Kegels im Schnittbild eine Gerade ist. Deshalb ist jede Scheibe um den Betrag R/n kleiner als die darunter liegende. Die unterste hat den selben Radius wie die Grundfläche des Kegels, also R. (Wer es lieber formaler hat, kann diesen Sachverhalt auch mit dem Strahlensatz beweisen: Die senkrechte Mittelachse des Kegels und die Schnittlinie der Mantelfläche sind die Strahlen, die Radien der Scheiben die Parallelen.)

Wenn wir die Scheiben von unten nach oben beginnend bei Null durchnummerieren ist also ihr jeweiliger Radius

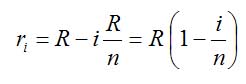
Das Volumen einer Scheibe mit der Nummer i ist also

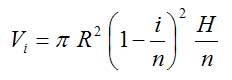
Das Volumen aller Scheiben zusammen, also unsere Näherung für das Kegelvolumen ist demnach

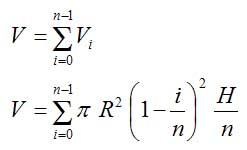
Das komische eckige Zeichen Σ ist der große griechische Buchstabe Sigma und bedeutet nichts anderes als Summe. Damit man nicht so viel schreiben muss, kann man Summen, deren Summanden sich nur an wenigen Stellen unterscheiden, auf diese Weise schreiben. Die Stellen, an denen etwas anders ist, werden mit einem Platzhalter - in obigem Beispiel mit dem Buchstaben i - versehen und über und unter das Summenzeichen schreibt man, welche Werte dieser Platzhalter in den einzelnen Summanden annimmt. Ein einfaches Beispiel:

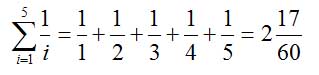
Wenn in einer Summe bei jedem Summanden der selbe Faktor steht, kann man ihn ausklammern. Das betrifft alle Größen außer dem i, denn das ist ja in jedem Summanden anders.
In unserer Rechnung können wir alle Größen außer der Klammer vor das Summenzeichen ziehen, also ausklammern:

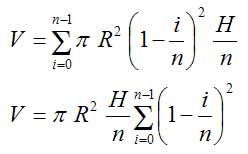
Auf die Klammer wenden wir nun die zweite binomische Formel an, d.h. wir multiplizieren das Quadrat aus:

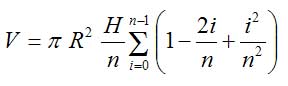
Jetzt schreiben wir die Summanden hinter dem Summenzeichen Σ alle als separate Summen. Dabei klammern wir in jeder einzelnen Summe wieder alles aus, was geht:

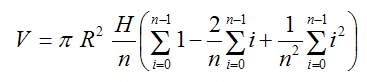
Die erste Summe ist besonders einfach, denn wir addieren die Zahl 1 n Mal auf, rechnen also

1 _(i=0) + 1 _(i=1) + 1 _(i=2) + 1 _(i=3) + ... + 1 _(i=n) = n

Und nun kommt ein Trick:
Bei der nächsten Summe sollen wir alle Zahlen bis n-1 aufaddieren. Stellen wir uns vor, wir sollten die Zahlen von 1 bis 100 zusammenrechnen.

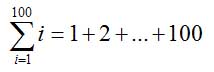
Dafür können wir uns das Leben einfach machen, indem wir die Summanden umsortieren und immer Paare bilden, die die selbe Summe ergeben:

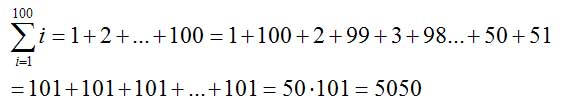
Allgemein kann man sagen, dass es immer halb so viele Paare gibt wie Zahlen, die aufaddiert werden sollen, und dass die Summe, die jedes Paar ergibt, immer gleich der größten Zahl plus eins ist. Um auf unsere Summe zu kommen müssen wir jetzt nur noch die Anzahl Paare mit dem Wert der Paarsumme multiplizieren:

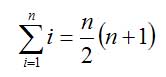
Diese Formel heißt übrigens "Der kleine Gauß", weil Carl Friedrich Gauß sie als Schüler herausgefunden herausgefunden hat.

Nun müsste der Einwand kommen, dass diese Herleitung nur für gerade Zahlen funktioniert, weil ja sonst bei der Paarbildung eine Zahl übrig bleibt. Wir überprüfen unsere Formel also für ungerade n, indem wir in die Formel (n-1), was ja dann eine gerade Zahl ist, statt n einsetzen und zum Ergebnis das ungerade n hinzuaddieren:

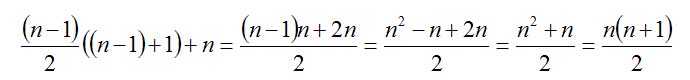
Wir sehen also: Es kommt für gerade und für ungerade n die selbe Formel heraus!

Für die Summe der Quadratzahlen 1 + 4 + 9 + ... + n² gibt es eine ähnliche Formel, die aber nicht ganz so einfach herzuleiten ist:

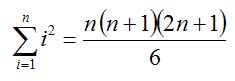
Wer wissen will, wie man darauf kommt, der findet bei Arndt Brünner eine prima Erklärung.

Nun wollen wir die in unserem kleinen Exkurs kennen gelernten Formeln aber auch anwenden. Das heißt wir setzen die beiden Formeln an Stelle der Summen:

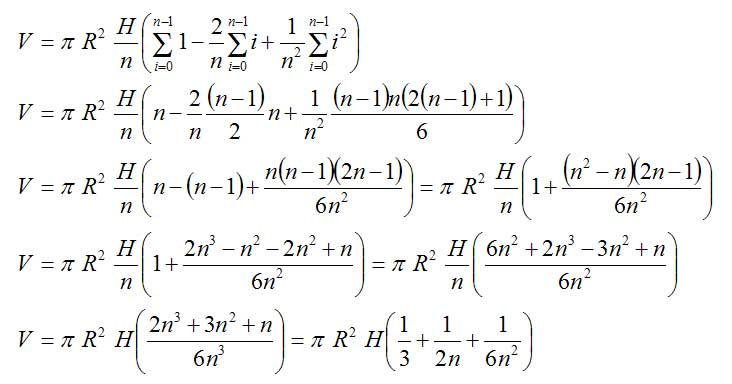
Das ist die Formel für das Volumen unseres Treppenkegels. Wir können die Plausibilität prüfen, indem wir n=1 einsetzen, den Kegel also durch einen Zylinder "annähern": Und siehe da, es kommt die Formel für das Volumen des Zylinders heraus, weil der Klammerausdruck eins wird.

Jetzt kommt noch ein letzter Schritt, denn ursprünglich wollten wir ja das Volumen des glatten Kegels wissen, nicht des Treppenkegels: Wir können uns überlegen, dass wir dem glatten Kegel umso näher kommen, je mehr Scheiben wir für die Näherung verwenden, je größer wir also n machen, denn der Fehler, den wir in der Treppenrechnung machen, entspricht ja den kleinen grünen Treppenstufen in obigem Bild und die werden umso kleiner, je größer n wird; ihre Breite ist nämlich R/n und ihre Höhe H/n.

Die Formel für das Kegelvolumen erhalten wir also, wenn wir in der oben stehenden Treppenformel n gegen unendlich gehen lassen:

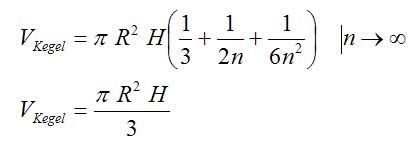
Wie wir oben schon gesagt haben, funktioniert das Berechnungsverfahren auch für Pyramiden. Wir müssen nur statt der Kegelgrundfläche π R² die Pyramidengrundfläche einsetzen. Das Volumen einer Pyramide berechnet sich also zu

V_Pyramide = Grundfläche · Höhe / 3