Einleitung

Bei meiner Arbeit als Nachhilfelehrer für Mathematik stelle ich immer wieder fest, dass der Grund für die Verständnisschwierigkeiten meiner Schüler weniger beim aktuell behandelten Stoff selbst – wie zum Beispiel Integral- und Differentialrechnung oder Stochastik – liegt, sondern dass ihnen einfache Grundlagen fehlen, die sie benötigen, um die Herleitung dieses Stoffes nachvollziehen und die erlernten Werkzeuge einüben zu können.

Mit Abstand am häufigsten fehlen Kenntnisse und Fertigkeiten des Bruchrechnens.

Mit diesem Kompendium möchte ich eine kompakte Möglichkeit bieten, die Ideen hinter dem Bruchrechnen und die Bedeutung der verschiedenen Begriffe und Schreibweisen zu verstehen. Im Anschluss daran sollten unbedingt Aufgaben gerechnet werden, um das erlangte Verständnis durch Übung zu vertiefen und dauerhaft zu verankern. Entsprechende Aufgaben finden sich reichlich im Internet.

Da diese "Seite" etwas länger geworden ist, gibt es sie hier auch als pdf zum Herunterladen.

Mathematiker sind bequem und faul! Sie machen sich alles so einfach wie möglich – auch und gerade bei der Bruchrechnung:

Nehmen wir die Divisionsaufgabe

oder anders geschrieben

oder noch anders

Um diese Aufgabe einfacher rechnen zu können, kann man sie in eine einfache und eine schwierige Aufgabe zerlegen:

Den ersten Teil der Aufgabe können wir seit der Grundschule rechnen, das Ergebnis ist 3. Und den zweiten Teil? Der ist uns zu schwierig! Den rechnen wir gar nicht aus! Den lassen wir einfach stehen:

Die letzte Schreibweise $3\frac{1}{3}$ ist ein weiterer Beweis für die Faulheit der Mathematiker: Sie lassen das Pluszeichen einfach weg und nennen das Ganze eine Gemischte Zahl.

Man kann einen Bruch also auch wie folgt auffassen:

Ein Bruch steht für die Zahl, die herauskäme, wenn man die obere Zahl durch die untere teilen würde; ein Bruch ist eine nicht gerechnete Divisionsaufgabe.

Ist die obere Zahl größer als die untere, spricht man von einem unechten Bruch, den man in eine gemischte Zahl umrechnen kann.

Bei einem echten Bruch ist die obere Zahl immer kleiner als die untere.

Man nennt Bruchzahlen auch Rationale Zahlen, weil sie ein Verhältnis zweier Zahlen ausdrücken (lat. ratio = Berechnung, Verhältnis, Vernunft, ...).

Wenn die obere Zahl "1" lautet, kann man sich eine schöne bildliche Vorstellung der Bedeutung dieses Bruchs machen:

$\frac{1}{5}$ bedeutet zum Beispiel: Teile ein Ganzes in fünf gleich große Teile!
Einen solchen Bruch, bei dem $11$ geteilt wird, nennt man auch Stammbruch.

In nachfolgendem Comic ist Obelix' Tortenstück kein Stammbruch! (Quelle: René Goscinny und Albert Uderzo: "Asterix und Kleopatra", Text modifiziert)

Zähler und Nenner

Weil man Äpfel nur mit Äpfeln vergleichen soll, ist das Ganze, das bei einem solchen Bruch geteilt wird (die 10 in Gleichung (5) oder die 1 bei einem Stammbruch), immer gleich, d.h. ein Drittel des einen Apfels ist in der Mathematik das gleiche wie ein Drittel eines anderen Apfels. Und weil die Bruchteile des Ganzen per Definition untereinander auch alle gleich sind (s. oben!), spielt es keine Rolle, ob ich z.B. von einem Ding zwei Bruchteile nehme, oder ob ich von zwei gleichen Dingen jeweils ein Bruchteil nehme:

Links haben wir ein Fünftel eines Apfels plus ein weiteres Fünftel dieses Apfels genommen (zwei gleiche Bruchteile von einem Ding).

Das ist dasselbe wie eine Multiplikation mit 2, denn Multiplikation ist nichts anderes als Zählen, wie oft man die selbe Zahl addiert. Diese Multiplikation steht bei Gleichung (6) in der Mitte.

Rechts steht, was wir erhalten, wenn wir zwei Äpfel als das zu teilende Ganze betrachten und in fünf gleiche Teile teilen.

Weil das alles dasselbe ist und weil man mit der oberen Zahl gewissermaßen zählt, wie viele gleiche Bruchteile man von einem Ganzen nimmt oder von wie vielen gleichen Dingen man jeweils den gleichen Bruchteil nimmt, nennt man diese obere Zahl den Zähler des Bruchs.

Die untere Zahl benennt, was für ein Teil wir von dem oder den Ganzen nehmen. Diese Zahl heißt deswegen der Nenner des Bruchs; sie sagt uns, wie groß die einzelnen Bruchteile sind.

ACHTUNG: Je größer der Nenner eines Bruchs ist, desto kleiner ist der Bruchteil, weil die Zahl ja bedeutet, wie viele gleiche Teile ein Ganzes ergeben, und je mehr Teile man aus einem Ganzen erzeugt, desto kleiner werden die Teile:

Multiplikation von Brüchen

Ganz nebenbei, haben wir mit (6) schon gelernt, wie man einen Bruch mit einer ganzen Zahl multipliziert:

Multiplizieren bedeutet, gleiche Teile zählen oder aufaddieren. Stammbrüche sind gleiche Teile, die durch einen Zähler gezählt werden.

Also muss beim Multiplizieren eines Bruchs sein Zähler mit dem Faktor multipliziert werden.

Was ist, wenn der Faktor selbst auch ein Bruch ist?

Warum sollte es dann anders sein?

Und was bedeutet der komische Doppelbruch am Ende? Als erstes nehmen wir Ganze und teilen sie durch vier. Mit sechs übereinander gestapelten Torten könnte das ungefähr so aussehen wie das gelbe Stück in folgender Zeichnung (wer nicht so gerne Torte ist, kann das Beispiel natürlich auch mit Pizza machen):

Danach teilen wir dieses Stück noch einmal durch drei, das sieht dann so aus:

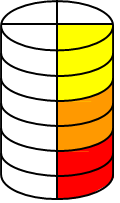
Das Stück, das dabei herauskommt, z.B. das rote, ist bezogen auf das ursprüngliche Ganze (die sechs gestapelten Torten) ein Zwölftel, weil zwölf dieser gleichen Stücke wieder das Ganze ergeben. Wieso Zwölftel? Weil wir erst durch $3$ und dann durch $4$ geteilt haben und wir die gleichen Stücke zählen, also multiplizieren.

Unsere Rechenaufgabe von oben können wir also so fortsetzen:

Kleiner Merksatz für solche Doppelbrüche:
Wenn im Zähler ein Bruch steht, kann man den „durchsacken“ lassen, also den Nenner des oberen Bruchs als Faktor mit in den Nenner schreiben.

Daraus ergibt sich folgende Regel:

Brüche multipliziert man miteinander, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert.

Genauso wie wir gezeigt haben, dass der Satz für ganze Zahlen auch für Brüche gilt, können wir auch zeigen, dass dieser Satz für Brüche auch für ganze Zahlen gilt, denn eine ganze Zahl kann man immer auch als Bruch mit dem Nenner $1$ schreiben:

Division von Brüchen

Ganz oben – in Gleichungen (1) bis (5) – haben wir uns schon klar gemacht, dass ein Bruch schon eine Divisionsaufgabe ist. Eine Zahl – z.B. $3$ – durch z.B. $4$ zu teilen, bedeutet nichts anderes, als sie mit $\frac{1}{4}$ malzunehmen:

Eine Divisionsaufgabe (zur Erinnerung: $\text{Dividend : Divisor = Quotient}$) entspricht folgender Aussage: Der Quotient sagt uns, wie oft der Divisor in den Dividenden hineinpasst: bedeutet, dass die $3$ fünf Mal in $15$ hineinpasst, wir sie also fünf Mal aufaddieren, also mit $5$ malnehmen können und $15$ erhalten.

Der Nenner eines Bruches sagt uns aber doch auch, in wie viele gleiche Teile ein Ganzes zerlegt wurde. Wenn wir also $1$ Ganzes durch $\frac{1}{3}$ teilen, also uns die Frage stellen, wie oft das Drittel in $1$ passt, dann ist die Antwort doch gerade der Nenner, also in diesem Fall $3$ Mal; und wenn wir $5$ durch $\frac{1}{3}$ teilen, ist die Antwort $5·3$. Wir müssen also den Dividenden mit dem Nenner des Divisors multiplizieren.

Wollen wir statt durch $\frac{1}{3}$ durch $\frac{2}{3}$ dividieren, passt dieser doppelt so große Divisor natürlich nur halb so oft in die $5$ hinein, also müssen wir das Ergebnis noch durch den Zähler $2$ dividieren.

Beides zusammen ergibt folgende Rechenregel:

Man teilt durch einen Bruch, indem man mit seinem Kehrwert multipliziert.
Kehrwert ist derjenige Bruch, bei dem Zähler und Nenner genau vertauscht sind.

Erweitern und Kürzen

Verschiedene Rechenaufgaben können ja durchaus mal dasselbe Ergebnis haben, oder? Zum Beispiel ist:

Bei Brüchen (= Divisionsaufgaben! Siehe (12c)) ist das immer dann der Fall, wenn Dividend und Divisor (also Zähler und Nenner!) mit derselben Zahl multipliziert oder durch die selbe Zahl dividiert wurden; im Beispiel (12c) wurde der Zähler durch $2$ geteilt () und der Nenner ebenso ().

Warum ist das so?

Teilt man eine Zahl durch sich selbst, so ist das Ergebnis immer $1$. Ein Bruch, dessen Zähler und Nenner gleich sind, hat also immer den Wert $1$.

Die Zahl $1$ nennt man auch das neutrale Element der Multiplikation und der Division. Das bedeutet, dass eine Multiplikation mit $1$ oder eine Division durch $1$ den anderen Operanden nicht verändert. Ich darf also jede Zahl mit $1$ multiplizieren, ohne sie dadurch zu verändern. Also darf ich auch jede Zahl mit irgendeinem Bruch multiplizieren, dessen Zähler und Nenner gleich sind. Zeile (12c) kann man also auch so schreiben:

Diesen Vorgang, Zähler und Nenner eines Bruchs mit der selben Zahl zu multiplizieren, nennt man Erweitern des Bruchs.

Wir werden das Erweitern später für die Addition von Brüchen benötigen.

Man kann sich leicht überlegen, dass man Zähler und Nenner auch durch eine Zahl dividieren darf:

Die einfachste Erklärung ist die, dass ich einen zuvor erweiterten Bruch wieder in den ursprünglichen verwandeln können muss, und das geschieht, indem ich Zähler und Nenner durch eben diese Zahl, mit der ich zuvor erweitert habe, dividiere.

Es gibt aber noch eine andere Erklärung:

Jede ganze Zahl – also auch Zähler und Nenner eines Bruchs – lässt sich als Produkt von Primzahlen darstellen („Primfaktorzerlegung“).
Eine Primzahl ist eine Zahl, die durch genau zwei Zahlen ohne Rest dividiert werden kann, nämlich durch 1 und durch sich selbst. Beispiele für Primzahlen sind $2$, $3$, $5$, $7$, $11$, …, $647$.
Andere Zahlen heißen zusammengesetzte Zahlen. $6$ ist z.B. eine zusammengesetzte Zahl, weil sie außer durch $1$ und $6$ auch durch $2$ und $3$ teilbar ist.

Kommen nun in Zähler und Nenner ein oder mehrere gleiche Primfaktoren vor, kann man diese zu Brüchen mit identischem Zähler und Nenner kombinieren; diese Brüche haben den Wert $1$, können also aus dem Produkt weggelassen werden (→ neutrales Element). Das Entfernen eines Faktors aus der Primfaktorzerlegung ist aber nichts anderes als die Division durch denselben.

Beispiel:

Diesen Vorgang, Zähler und Nenner durch dieselbe Zahl zu dividieren, nennt man Kürzen des Bruchs.

Das Kürzen ist sehr hilfreich, weil die Zahlen im Zähler und im Nenner dadurch kleiner werden und so das Weiterrechnen vereinfacht wird. Es ist eine gute Angewohnheit, vor und nach einer Multiplikation alle beteiligten Brüche so weit es geht zu kürzen!

Potenzieren von Brüchen

Potenzieren bedeutet: "Zählen wie oft man eine Zahl mit sich selbst multipliziert":

Wenn wir Brüche potenzieren wollen, müssen wir also die Regel für das Multiplizieren anwenden und erhalten:

Bei einer Potenz nennt man die Zahl, die unten steht, Basis und die Zahl, mit der man zählt, wie oft die Basis mit sich selbst multipliziert wird, heißt Exponent.

Was passiert nun, wenn ein Bruch aus Potenzen gleicher Basis aber unterschiedlichem Exponenten besteht?

Man kann mit der Basis kürzen! Und zwar nicht nur mit der Basis, sondern mit der kleineren ihrer vorkommenden Potenzen. Weil das so ist, kann man Potenzen, die im Nenner eines Bruchs vorkommen, auch in den Zähler schreiben und dabei das Vorzeichen des Exponenten wechseln:

Addition von Brüchen

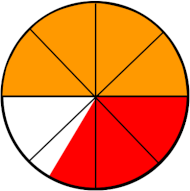
Gestern dachte ich zunächst, ich hätte nicht besonders viel Hunger, und habe deshalb erst mal nur eine halbe Pizza (im Bild unten orange eingefärbt) gegessen. Die war aber so lecker, dass ich danach doch noch ein Drittel (rot) verschlungen habe. Wie viel Pizza habe ich insgesamt gegessen?

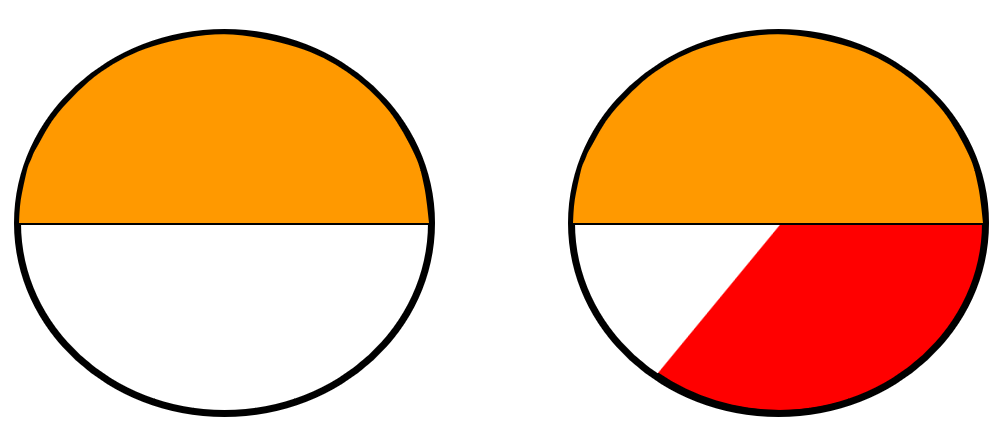
Aus dem Stegreif fällt es uns schwer, diese Frage zu beantworten, oder?

Ist es mit nachfolgender Abbildung einfacher?

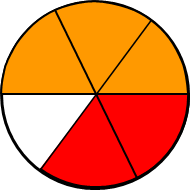
Ich finde schon! Was ist passiert? Ich habe die Hälfte und das Drittel in jeweils gleich große Teile unterteilt. In diesem Beispiel sind das Pizza-Sechstel. Die kann man dann ganz einfach zusammenzählen: Die Hälfte besteht aus drei Pizza-Sechsteln, und das Drittel aus zweien. Also habe ich insgesamt $3+2=5$ Pizza-Sechstel gegessen.

Aber warum ausgerechnet Sechstel? Hätte das Ganze nicht auch mit Achteln funktioniert?

Nein! Warum nicht? Weil man das Drittel nicht in ganzen Achteln ausdrücken kann! Ein Pizza-Drittel sind nämlich $2\frac{2}{3}$ Pizza-Achtel!

Um zwei Brüche (hier die Pizzahälfte und das Pizza-Drittel) einfach addieren zu können, müssen wir die Bruchteile so weiter unterteilen, dass sich beide durch eine ganzzahlige Menge noch kleinerer Bruchteile darstellen lassen. Das ist genau dann der Fall, wenn der Nenner der kleinen Bruchstücke (im Beispiel die Pizza-Sechstel, also $6$) sich durch die Nenner beider anderen Brüche teilen lässt; der gesuchte Nenner ist also ein Vielfaches der beiden anderen.

Weil wir nicht mehr teilen wollen als unbedingt notwendig – wir wollen ja nicht mit unnötig großen Zahlen rechnen –, suchen wir einen möglichst kleinen Nenner, also das kleinste gemeinsame Vielfache der Nenner der beiden Brüche die wir addieren wollen.

Dieses kleinste gemeinsame Vielfache (oder kurz kgV) kann man aus der Primfaktorzerlegung bestimmen: Es ist das Produkt aller Primfaktoren, die insgesamt in beiden Zerlegungen vorkommen, anders gesagt: das Produkt der jeweils höchsten vorkommenden Potenz aller Primfaktoren.

Beipiel:
Berechnung des kleinsten gemeinsamen Vielfachen von $140$ und $1050$:

Wenn das Berechnen des kgV schwieriger ist als das Weiterrechnen mit großen Zahlen, können wir auch auf die Bedingung verzichten, dass unser neuer Nenner so klein wie möglich sein soll. In diesem Fall nehmen wir einfach das Produkt der beiden Nenner, denn das lässt sich ja auf jeden Fall durch beide teilen. Wenn wir mit Variablen rechnen anstatt mit Zahlen, bleibt uns ohnehin nichts Anderes übrig.

Zurück zum Beispiel:

$\frac{1}{2}$ und $\frac{1}{3}$ können wir addieren, indem wir das kgV von $2$ und $3$ suchen; das ist $6$.
(Hier kommen wir mit der Methode der Primfaktorzerlegung zum selben Ergebnis wie mit der Produktmethode, weil beide Nenner Primzahlen sind.)
Deshalb müssen wir die beiden Brüche wie auch an obigen Bildern schon gezeigt in Sechstel umrechnen.

Um zwei Brüche addieren (oder subtrahieren) zu können, muss man sie auf denselben Nenner, den sogenannten Hauptnenner, erweitern.
Der Hauptnenner ist ein gemeinsames Vielfaches der beiden Nenner der Summanden, z.B. das kleinste gemeinsame Vielfache oder ihr Produkt.

Das Umrechnen geht ganz einfach mit dem oben beschriebenen Erweitern (12d): Wir multiplizieren Zähler und Nenner jedes Bruchs mit derjenigen Zahl, die herauskommt, wenn man den Hauptnenner durch seinen Nenner teilt:

Hier das Verfahren zur Addition von Brüchen noch einmal zusammengefasst:

Subtrahieren ist dasselbe wie Addieren, nur dass der zweite Summand negativ ist.

Ein Bruch ist negativ, wenn Zähler und Nenner unterschiedliche Vorzeichen haben; haben sie gleiche Vorzeichen, ist der Bruch positiv – genau wie bei einer Divisionsaufgabe eben.

Bruchterme

Damit haben wir jetzt alle vier Grundrechenarten mit Brüchen durchgenommen. Was jetzt noch übrig bleibt, sind Kombinationen davon. Um damit richtig umzugehen, muss man sich nur an die üblichen Rechenregeln wie Punkt- vor Strichrechnung halten und folgendes Wissen:

Ein Bruchstrich unter oder über einer Summe ist dasselbe wie eine Klammer um diese Summe!

Beipiel:

aber bei der Multiplikation sieht das anders aus, vgl. (6):

Dieser Unterschied zwischen (20) und (21) ist wichtig! Meines Erachtens ist das die häufigste – und doch so einfach zu vermeidende – Fehlerquelle beim Bruchrechnen.

Nun noch eine Zusammenfassung mit Variablen statt mit Zahlen:

Weitere Erscheinungsformen von Brüchen

Prozent

Eine andere Schreibweise für einen Bruch ist das Prozentzeichen!

Die Bezeichnung Prozent kommt aus dem Lateinischen:

pro = für
centum = hundert

Das Zeichen % ist aus der Abkürzung cto für cento (italienisch für Hundert) entstanden.

Wenn jemand „23%“ sagt, bedeutet das so viel wie $\frac{23}{100}$ oder in Textform:

„Wenn die Gesamtheit 100 wären, dann wäre der Anteil 23.“

Daraus wird klar, dass eine Prozentangabe nur im Zusammenhang mit einer Bezugsgröße sinnvoll ist: „Das sind 23% von ...“

Beim Prozentrechnen ist es immer wichtig, sich die Bezugsgröße klarzumachen!

(vgl. Melonenrätsel am Ende des Kompendiums!)

Das Problem der Bezugsgröße tritt auch auf, wenn es z.B. heißt:

"Die zwei Teile eines Ganzen stehen im Verhältnis $2$ zu $3$."

Bei dieser Aussage ist die Bezugsgröße für den einen Teil der andere Teil: Der eine Teil ist $\frac{2}{3}$ des anderen Teils.
Wenn man mit diesen Größen weiterrechnen will, möchte man sie aber in aller Regel auf das Ganze, also die Summe beider Teile beziehen und dann ist der eine Teil $\frac{2}{5}$ des Ganzen und der andere ist $\frac{3}{5}$ des Ganzen. Aufpassen!

Beispiel:

Gegeben ist die Strecke a zwischen den Punkten A und B.
Diese Strecke wird durch den Punkt P im Verhältnis 2 zu 3 geteilt.
Wie lang ist die Strecke x, die von P zum näher gelegenen Endpunkt von a geht?

Antwort:

Dezimalbruch

Hand auf’s Herz! Bevor du dich mit diesem Kompendium beschäftigt hast, hast du es bestimmt oft vermieden, so mit Brüchen zu rechnen, wie wir es oben getan haben, oder? Dezimalzahlen („Kommazahlen“) waren dir bestimmt immer sympathischer als Brüche.

Dabei sind Dezimalzahlen auch nichts anderes als Brüche! Man spricht sogar oft von Dezimalbrüchen!

Was muss man tun, um einen Bruch in eine Dezimalzahl umzurechnen?

Diese Frage kannst du ganz einfach beantworten, wenn du dir den ersten Abschnitt dieses Kompendiums in Erinnerung rufst: Ein Bruch ist eine nicht gerechnete Divisionsaufgabe. Wenn wir diese Divisionsaufgabe lösen, erhalten wir das Ergebnis als Dezimalzahl.

Man wandelt einen Bruch in eine Dezimalzahl um, indem man den Zähler durch den Nenner dividiert.

Beispiel:

In diesem Fall geht die Rechnung sehr schön und nach wenigen Kommastellen auf. Das ist leider nicht immer der Fall. Es gibt sogar Brüche, deren Darstellung als Dezimalzahl unendlich lang ist! Wie umständlich! Aber eine kleine Rettung gibt es dabei: Wenn ein Bruch zu einer unendlich langen Dezimalzahl führt, wiederholt sich die Zahlenfolge entweder sofort nach dem Komma oder nach endlich vielen Nachkommastellen.

Beispiele:

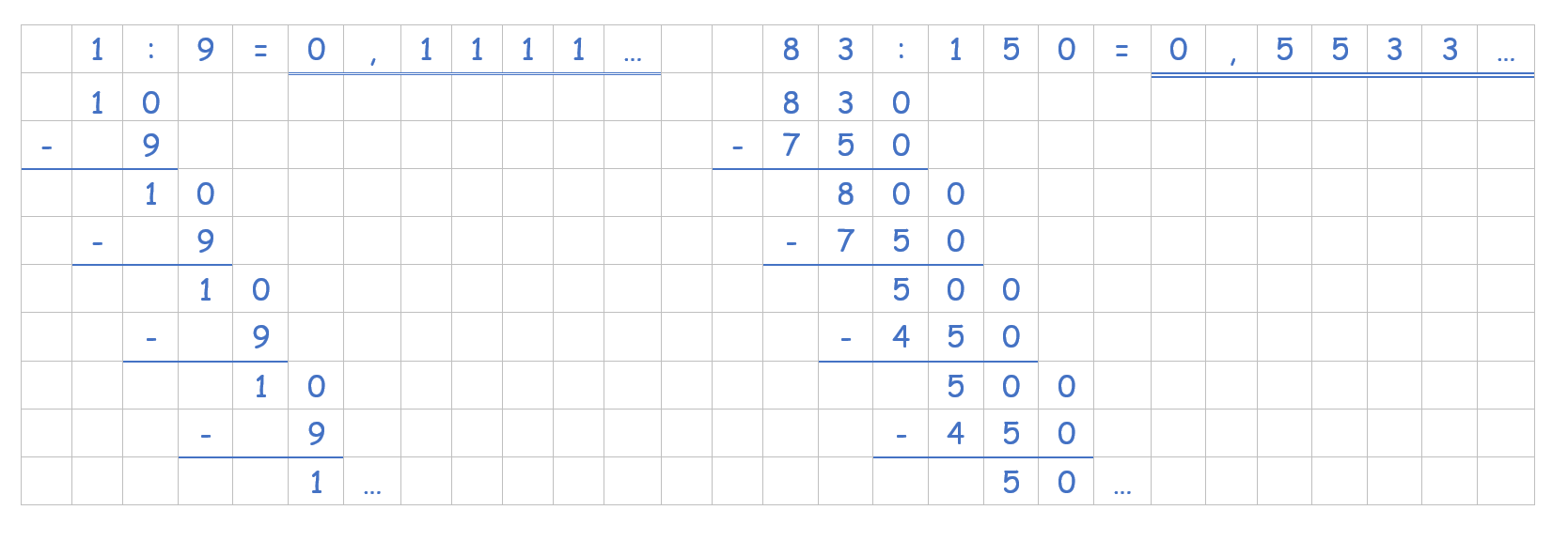
Die sich wiederholenden Zahlen schreibt man mit einem Strich oben drüber. Man spricht die Zahl $0,553$ dann aus als „Null Komma Fünf Fünf Periode Drei“.
Das Wort „Periode“ sagt man zum Beginn der Periode, weil anderenfalls nicht eindeutig wäre, wo die Periode beginnt.

Die Rechnungen verdeutlichen, wie die Periode entsteht: Ab einem bestimmten Punkt der Rechnung bleibt immer derselbe Rest.

Wenn man einen Bruch als Dezimalzahl darstellt, hat diese entweder endlich viele Nachkommastellen oder nach einer endlichen Zahl von Nachkommastellen wiederholt sich die Zahlenfolge. Solche Zahlen heißen rationale Zahlen.

Unendlich lange, nicht periodische Dezimalzahlen lassen sich nicht als Bruch darstellen! Sie heißen irrationale Zahlen.
Beispiel: Die Kreiszahl π = 3.14159…, die dem Verhältnis von Durchmesser zu Umfang jedes Kreises entspricht.

Umrechnungen

Wie rechnet man nun eine Dezimalzahl in einen Bruch um?

Dazu überlegen wir uns, welche Bedeutung die Stellen einer Dezimalzahl haben:

Der einzige Unterschied zu den bisher verwendeten Brüchen ist der, dass die Nenner immer Potenzen von $10$ sind.

Wenn man das weiß, kann man Dezimalzahlen in Brüche umrechnen, indem man ganz einfach den Dezimalbruch kürzt.
(Der Einfachheit halber bestehen die folgenden Beispiele jetzt nur noch aus echten Brüchen, d.h. die Dezimalzahlen haben keinen ganzzahligen Anteil bzw. bei den Brüchen sind die Zähler immer kleiner als die Nenner. Für die Rechnung mit unechten Brüchen bzw. gemischten Zahlen muss man nur den ganzzahligen Anteil dazu addieren.)

Eine nicht periodische Dezimalzahl wandelt man in einen Bruch um, indem man die Nachkommastellen zum Zähler macht und den Nenner als 1 mit so viel Nullen schreibt, wie die Dezimalzahl Nachkommastellen hat.
Anschließend kürzt man so weit wie möglich.

(Oder vornehmer ausgedrückt: Der Nenner ist eine Potenz von $10$, deren Exponent der Anzahl Nachkommastellen der Dezimalzahl entspricht.)

Schwierig bzw. unmöglich wird dieses Vorgehen, wenn wir eine unendliche, periodische Dezimalzahl in einen Bruch umrechnen müssen. Wie man dann vorgehen muss, möchte ich anhand von Beispielen erklären:

Beginnen wir einfach mit der Dezimalzahl $d=0,123$:

Als erstes multiplizieren wir diese Zahl mit einer Zehnerpotenz, die der Länge der Periode entspricht: Hier umfasst die Periode drei Stellen, so dass wir mit ${10}^3=1.000$ multiplizieren müssen:

Danach ziehen wir auf beiden Seiten dieser Gleichung die ursprüngliche Zahl $d$ ab und dividieren durch die so entstehende Neunerzahl, hier also durch $999$:

Eine sofort periodische Dezimalzahl wandelt man in einen Bruch um, indem man die Periode durch die „Neunerzahl“ der Periodenlänge teilt.

Wenn die Periode erst weiter hinter dem Komma beginnt, wird die Rechnung noch umständlicher, denn wir müssen den periodischen und den nicht periodischen Teil separat umwandeln. Das lässt sich am besten anhand des folgenden Beispiels nachvollziehen:

Der nicht periodische Teil ist $\mathrm{0,55}$. Den wandeln wir wie zuvor beschrieben in einen Bruch um: Der Zähler $55$ hat zwei Stellen, also hat der Nenner ($100$) zwei Nullen.

Der periodische Teil $0,003$ ist leider immer noch nicht sofort periodisch, so dass wir den so als Produkt schreiben, dass der eine Faktor sofort periodisch ist:

Dann haben wir alle Teile so, dass wir sie mit den zuvor beschriebenen Methoden ausrechnen können.

Vor- und Nachteile von Brüchen und Dezimalzahlen

Zum Schluss noch ein Wort zu den Vor- und Nachteilen von Brüchen und Dezimalzahlen:

Dezimalzahlen haben den Vorteil, dass sie sich leicht vergleichen lassen. Das kann bei Brüchen schwieriger sein. Oder wüsstest du auf Anhieb zu sagen, welche der beiden folgenden Brüche größer ist?

$\frac{23}{175}\text{oder}\frac{7}{50}$

Tatsächlich ist es der zweite Bruch, was du in der Dezimaldarstellung sofort erkennen kannst:

Der zweite Bruch ist ein klein wenig größer als der erste, was du an der zweiten Nachkommastelle (der Hundertstel-Stelle) sofort sehen kannst.

Computer können mit Brüchen auch nicht so gut umgehen, weil sie ja keine Zahlen im eigentlichen Sinne sind, sondern eine Rechenaufgabe. Computer rechnen aber auch nicht mit Dezimalzahlen, sondern mit Binärzahlen, die nur aus Nullen und Einsen bestehen. Das näher zu erklären, würde aber über das Thema dieses Kompendiums hinausgehen.

Der Vorteil von Brüchen ist, dass man mit ihnen einfacher rechnen kann, wenn man keinen Taschenrechner zur Hand hat. Und man rechnet mit ihnen genauer, denn unendlich lange Dezimalzahlen muss man immer irgendwann runden. Auch Computer müssen das, so dass deren Ergebnisse auch ungenau sein können!

Außerdem muss man die Regeln des Bruchrechnens beherrschen, wenn man mit Variablen (also mit Platzhaltern für Zahlen, z.B. $x$) rechnen muss, denn wenn man keine Zahlen für Zähler und Nenner hat, kann man die Divisionsaufgabe, die der Bruch ist, natürlich nicht ausrechnen.

Beide Darstellungen haben also ihre Berechtigung.

Rätsel

Hier als Anhängsel noch zwei trickreiche Anwendungen der Bruchrechnung.

Nur Knobelfreaks müssen selbst auf die Lösung kommen, die anderen finden sie weiter unten.

Kamelherde

Ein Beduine, der $17$ Kamele besaß, ist gestorben und seinen drei Söhnen wird das Testament eröffnet:

Der älteste Sohn soll die Hälfte der Kamele erhalten.
Der zweitälteste Sohn darf immerhin noch ein Drittel sein Eigen nennen.
Der Jüngste war immer sehr ungehorsam und soll deswegen nur ein Neuntel der Kamele erhalten.

Die Brüder sind bestürzt über diese Verfügung, denn natürlich wollen sie keines der Kamele töten, nur um den Besitz teilen zu können!
Verzichten möchte aber natürlich auch niemand!

Wie können Sie dennoch den letzten Willen ihres Vaters erfüllen?

Ein Lkw bringt Wassermelonen von der Plantage zum Bahnhof. Zu Beginn der Fahrt wiegt die Ladung eine Tonne und die Melonen bestehen zu 99 % aus Wasser (deshalb heißen sie ja Wassermelonen).
Da es sehr heiß ist, verdunstet auf dem Weg zum Bahnhof ein Teil des Wassers, so dass der Wasseranteil, als der Laster am Bahnhof ankommt, nur noch 98 % beträgt.

Wie schwer ist die Melonenladung am Ende der Fahrt?

Kamelherde

Der Vater hat nicht sein gesamtes Vermögen testamentarisch festgelegt!

Wenn die Brüder auch das verbleibende Achtzehntel der Herde (also 17/18 Kamele!) unter sich aufteilen, können alle Kamele am Leben bleiben: Der älteste bekommt 9, der zweitälteste 6 und der jüngste 2 Kamele. Das sind zusammen 17!

Wassermelonen

Zu Beginn der Fahrt beträgt der Wasseranteil 99 % von 1.000 kg = 990 kg.
Dementsprechend beträgt der Fruchtfleischanteil 10 kg.

Am Ende der Fahrt hat sich das Gewicht des Fruchtfleischs nicht geändert: Es beträgt immer noch 10 kg.
Allerdings sind diese 10 kg nun 2 % des Gesamtgewichts, weil der Wasseranteil ja nur noch 98 % beträgt.
Das gesuchte Gesamtgewicht ist also dasjenige, von dem 10 kg 2 % entsprechen. Das sind 500 kg!

Man sieht, wie wichtig bei Prozentrechnung die Bezugsgröße ist!
Durch die unauffällige Änderung der Bezugsgröße (hier: des Gesamtgewichts) kann man die Hälfte aussehen lassen wie 1 %!
Das ist natürlich unseriös!