Beweis der Grenzwerte
Bei der Herleitung der Ableitung der Sinusfunktion tauchen zwei Grenzwerte auf:
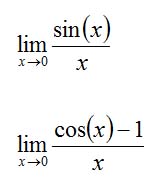
Welchen Wert sie annehmen, sieht man am leichtesten, wenn man die Funktionsgraphen betrachtet. Danach muss man natürlich noch einen mathematisch wasserdichten Beweis führen.
sin(x)/x
Man erkennt, dass egal von welcher Seite sich der x-Wert an Null annähert (von der positiven oder der negativen) der Funktionswert sich dem Wert 1 annähert. Der blaue Punkt im Bild markiert die Stelle.
N.B.: Es handelt sich übrigens um eine achsensymmetrische Funktion, obwohl nur sin und ungerade Potenzen von x darin vorkommen! Das zeigt, dass man sich bei Symmetriebetrachtungen von anderen Funktionen als Polynomen immer auf die Methode verlassen sollte, f(-x) zu berechnen und mit f(x) zu vergleichen.
Der Beweis wird hier geometrisch mit Hilfe eines Winkels α am Einheitskreis geführt:
Wir betrachten dazu ein blaues Dreieck ODC, dessen Höhe durch den Sinus des Winkels α gebildet wird.
Ferner den grünen Sektor des Einheitskreises, den der Winkel α ausschneidet (das "Tortenstück"), und drittens das rote rechtwinklige Dreieck ODE, dessen Höhe durch den Tangens des Winkels α gebildet wird.
Die Grundseite beider Dreiecke ist der Radius des Einheitskreises, also 1.
Michael Janßen, 22. Januar 2011, Erstellt mit GeoGebra
Die Fläche eines Dreiecks berechnet sich immer zu: ADreieck = 1/2 ˙ Grundseite ˙ Höhe
Die Fläche eines Sektors berechnet sich zu: ASektor = 1/2 ˙ α[rad] ˙ Radius
Aus der Zeichnung wird klar, dass das blaue Dreieck MBA immer kleiner ist als der grüne Sektor MBA und dieser wiederum immer kleiner ist als das rote Dreieck MBC.
Verschiebe den Punkt A mit der Maus auf dem Bogen des Einheitskreises, um dir das zu veranschaulichen. Du änderst dadurch den Winkel α.
Dieser Sachverhalt lautet in einer Formel ausgedrückt:
sin(α) / 2 < α / 2 < tan(α) / 2
Diese Ungleichungen multiplizieren wir zunächst mit 2:
sin(α) < α < tan(α)
Sodann erinnern wir uns, dass tan(α) = sin(α)/cos(α) und dividieren alles durch sin(α).
Das dürfen wir, ohne die Ungleichheitszeichen umzudrehen, weil wir zunächst nur positive Winkel betrachten, der Sinus also auch immer positiv ist. Später lässt sich leicht zeigen, dass die selbe Rechnung auch für negative Winkel funktioniert.
1 < α/sin(α) < 1/cos(α)
Nun bilden wir von allem den Kehrwert. Bei dieser Operation müssen die Ungleichheitszeichen verändert werden:
1 > sin(α)/α > cos(α)
Wenn wir nun α gegen Null gehen lassen, wird der Ausdruck, dessen Grenzwert wir suchen, zwischen der Konstante 1 und dem Wert cos(α=0) = 1 quasi eingequetscht, d.h. auch der Ausdruck sin(α)/α kann nur gegen 1 gehen.
Bei all diesen Betrachtungen ist α natürlich immer im Bogenmaß angegeben.
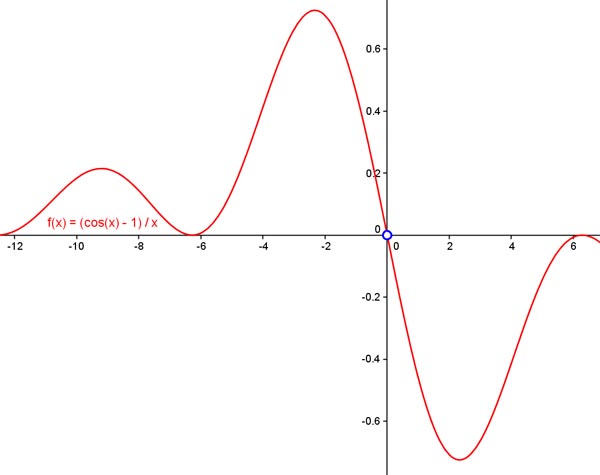
(cos(x)-1)/x