Ableitung, Tangente

In diesem Abschnitt geht es um ein Rechenverfahren, das Gottfried Wilhelm Leibniz und Isaac Newton unabhängig voneinander im 17. Hahrhundert entwickelt haben.
Dabei steht zuerst eine ganz unscheinbare Frage im Mittelpunkt der Betrachtung:

Welche Steigung hat die Tangente an eine Funktion f(x) im Punkt P(x₀ | f(x₀))?

Diese Frage scheint zunächst völlig aus der Luft gegriffen und hochgradig uninteressant; wer will das schon wissen???
Bei näherer Betrachtung erkennt man jedoch, dass die Tangente und insbesondere ihre Steigung Rückschlüsse auf die Funktion zulässt, die sie berührt: Zum Beispiel verläuft die Tangente nämlich an Extrempunkten (Maxima oder Minima) immer waagerecht, hat also die Steigung Null. Wenn wir uns nun vorstellen, dass eine Funktion unseren Gewinn in Abhängigkeit irgendeiner Einflussgröße darstellte, dann ist das Maximum dieser Funktion doch ein Punkt an dem wir stark interessiert wären! Genauso wollen wir das Minimum einer Funktion kennen, die z.B. den Kraftstoffverbrauch unseres Autos in Abhängigkeit (z.B.) der Geschwindigkeit darstellt.

Also ist die Frage nach der Steigung der Tangente doch nicht so uninteressant, wie wir vielleicht am Anfang gedacht haben.

Dieser Abschnitt leistet zunächst ein wenig Vorarbeit für die nachfolgenden, bei denen es dann darum geht, die Extrempunkte wirklich zu finden.

Tangenten sind Geraden, die eine Kurve in einem Punkt P(x₀|f(x₀)) berühren.
Geraden haben die Funktionsgleichung:

y = m · x + b

Dabei ist b der Schnittpunkt mit der y-Achse und m die Steigung. Der Zahlenwert dieser Steigung wird genauso berechnet wie im Straßenverkehr: Der Höhengewinn wird ins Verhältnis gesetzt zu der Strecke, auf der er erreicht wird. Bei einer Steigung von 12 % gewinnt man also z.B. auf 50 m Strecke eine Höhe von 6 m. Das Prozentzeichen, welches ja nichts anderes bedeutet als Hundertstel, lässt man bei Geraden weg und gibt den entsprechenden Zahlenwert an:

12 % = 0,12

Am einfachsten rechnet man eine Steigung also aus, indem man zwei Punkte auf der Geraden nimmt und ihren Höhenunterschied - das ist die Differenz der y-Koordinaten der beiden Punkte - durch ihren Abstand - die Differenz der beiden x-Koordinaten - dividiert. Bei einer Gerade durch die Punkte P₁(x₁|y₁) und P₂(x₂|y₂) berechnet sich die Steigung m zu:

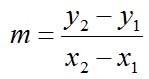
Diesen Ausdruck für die Steigung nennt man auch Differenzenquotient. (Ein Quotient ist das Ergebnis einer Division.)

Nachfolgendes Geogebra-Arbeitsblatt rekapituliert diese einfachen aber wichtigen Grundlagen noch einmal. Spiele mit den Schiebereglern, um zu sehen, welchen Einfluss m und b auf den Verlauf der Gerade haben!

Die Gerade an sich haben wir nun besprochen. Wir wollten uns aber ja mit einer besonderen Gerade befassen, der Tangente an eine Kurve.
Deren Besonderheit ist, dass sie die Kurve in genau einem Punkt P₀(x₀|f(x₀)) berührt. f(x) sei die Funktion, an deren Graphen wir die Kurve anlegen wollen.

Jetzt stehen wir erst mal da im kurzen Hemd: Wir brauchen zwei Punkte, um die Steigung der Tangente zu berechnen, haben aber nur einen. Was nun? Scheint ja nicht so zu klappen mit unserer Tangente.
Also vertagen wir unser Tangentenproblem und versuchen uns an etwas einfacherem: Wenn wir schon unbedingt zwei Punkte brauchen, um eine Steigung auszurechnen, dann berechnen wir eben die Steigung einer Geraden, die durch zwei Punkte geht, die beide auf dem Funktionsgraphen liegen. Eine solche Gerade nennt man Sekante.

Damit unsere Sekante wenigstens noch so ähnlich aussieht wie die Tangente, die wir eigentlich haben wollten, legen wir die beiden Punkte dicht nebeneinander; sagen wir mal, die beiden Punkte sollen mit ihren x-Koordinaten den Abstand h voneinander haben und h sei ziemlich klein.

Dann heißen unsere beiden Punkte:

P₀ (x₀ | f(x₀)) und P₁ (x₀+h | f(x₀+h))

Entsprechend obiger Formel für die Steigung können wir diese für die Sekante nun einfach berechnen:

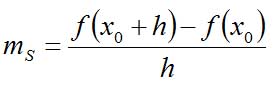
Probieren wir es gleich an unserem Einführungsbeispiel aus!
Zuerst die Zeichnung in Geogebra und danach die Berechnung.

Für die Rechnung werden hier die erste und zweite binomische Formel verwendet. Wer die nicht drauf hat, bitte noch mal nachlesen!

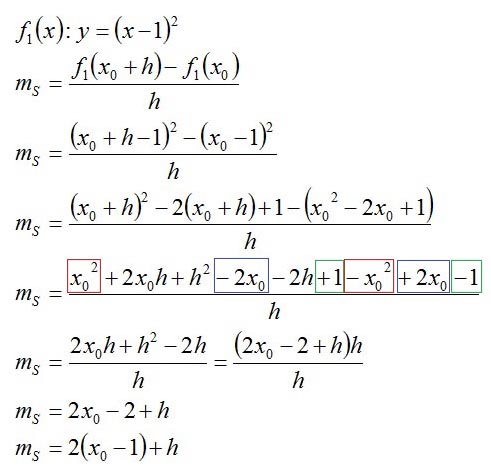
Jetzt haben wir also die Steigung der Sekante, die unsere Funktion bzw. ihren Graphen an der Stelle x₀ und an einer weiteren Stelle, die im Abstand h daneben liegt, schneidet.

Ursprünglich wollten wir aber doch mal die Steigung der Tangente m_T im Punkt P₀(x₀ | f(x₀)) ausrechnen. Hast du in obiger Zeichnung mit den Schiebereglern gespielt? Ist dir aufgefallen, dass die Steigung der Sekante m_S derjenigen der Tangente immer ähnlicher wird, je näher die beiden Punkte zusammenrücken?

Im Extremfall, wenn h Null wird, fallen die beiden Punkte zusammen und wir haben nur noch einen. Wenn wir in vorstehender Zeichnnung h=0 einstellen, wird aus der Sekante eine Tangente! Probiere es aus!

Was aber passiert mit der Steigung m_S, wenn h Null wird? HALT! ALARM!

h darf nicht Null werden, denn in der obigen Berechnung der Sekantensteigung haben wir durch h dividiert!

Naja, wir könnten ja mal schauen, was passiert, wenn h fast Null wird: So etwas nennt man einen Grenzwert. In der Mathematik heißt der genauso wie die Grenze der Römer gegen Germanien: Limes, abgekürzt lim und darunter schreibt man, wer sich wem an dieser Grenze annähert, in unserem Fall h → 0.

Also noch einmal deutlich zusammengefasst:

Die Steigung der Tangente an eine Kurve ist der Grenzwert des Differenzenquotienten der Sekantensteigung, bei dem der Abstand h der beiden Schnittpunkte gegen Null geht.

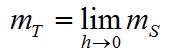
Für unser obiges Beispiel f₁(x) ergibt sich also für die Tangentensteigung:

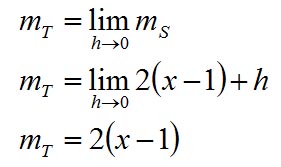
Das bedeutet zum Beispiel, dass die Tangente an f₁(x): y = (x - 1)² an der Stelle x₀ = 3 die Steigung m_T = 4 hat, an der Stelle x₀ = 2 die Steigung m_T = 1 usw.

Letztlich haben wir damit auch wieder eine Funktion: Jeder Stelle x₀, die wir uns vorstellen können, wird genau ein Wert zugewiesen, nämlich die Steigung der Tangente an f₁(x) an dieser Stelle. Diese Funktion nennt man die Ableitung von f₁(x) und schreibt sie als f₁'(x), sprich: "f 1 Strich von x".

Die Rechnerei mit dem Differenzenquotienten war ziemlich umständlich, oder? Außerdem gibt es ja noch viel, viel mehr Funktionen als das eine Beipiel, das wir hier gerechnet haben. Kann man das nicht einfacher machen? Man kann! Wenn man sich nämlich die Rechnerei mit den Differenzenquotienten immer wieder genau ansieht, findet man Regeln, wie sich das Endergebnis bildet. Diese Regeln werden auf der nächsten Seite hergeleitet.