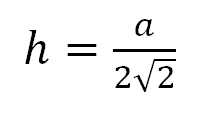Über Bienen gibt es viel zu erzählen. Viel Beeindruckendes gibt es zum Beispiel in dem Film More than honey.
Hier soll es - natürlich - um einen Zusammenhang zur Mathematik gehen. Dabei will ich gar nicht viel (vor-)rechnen sondern es geht mir hier um die räumliche Vorstellungskraft. Das Rechnen hat schon Professor Tim Grams erledigt, aber dazu später mehr.
Bienen produzieren Honig. Diesen lagern sie in ihrer Behausung, den Bienenwaben, ein. Diese Waben bestehen aus Wachs, das die Bienen selbst produzieren. Wer kennt nicht die herrlich duftenden Bienenwachskerzen vom Weihnachtsmarkt?!
Die Wachsproduktion ist für die Bienen sehr aufwändig und mühsam. Deswegen ist es für sie sehr wichtig, sparsam damit umzugehen. Wie genau sie das tun und bis in welches kleinste Detail, darum geht es auf dieser Seite.
Was bedeutet "sparsam" im Zusammenhang mit dem Bau von Lagerraum? Es bedeutet, mit möglichst wenig Materialverbrauch ein möglichst großes Volumen zu schaffen.
Die Form mit dem optimalen Verhältnis von Volumen zu Oberfläche ist die Kugel. Bei den Bienen gibt es allerdings noch weitere Optimierungskriterien: Beispielsweise die Haltbarkeit der Konstruktion und die Notwendigkeit, mehrere Behälter unmittelbar nebeneinander zu bauen, weil die Bienen nicht nur ihren Honig sondern auch ihre Nachkommenschaft "einlagern" wollen. Und wer mehrere Kinder hat, weiß, dass es gut ist, für jedes Kind ein eigenes Zimmer zu haben - und die Bienen haben viele Kinder!
Außerdem wäre eine Zugangsmöglichkeit ganz praktisch, die einer rundherum geschlossenen Kugel fehlt.
Deswegen ist eine an einer Seite geöffnete, "irgendwie zylindrische" Form die nächstbeste Wahl.
"Irgendwie zylindrisch" ist erst mal nicht sehr mathematisch. Von den Körpern, die in der Sprache der Mathematik vorkommen, trifft es das Prisma am besten. (Wer sich der Definition nicht sicher ist, lese bitte hinter dem Link nach!)
Wie bringt man nun ganz viele Prismen möglichst platzsparend nebeneinander unter?
Zuerst vereinfachen wir das Problem, indem wir uns vorstellen, wir blickten senkrecht von oben auf die Öffnungen der "Lagerräume". Dann reduziert sich das Problem, welche Grundflächen wir für die Prismen verwenden wollen, auf die Frage, welche Flächenformen im Verhältnis zu ihrem Umfang den größten Flächenanteil bedecken.
Sollen die "Lagerräume" beispielsweise Zylinder sein, die ja einzeln betrachtet ein besonders gutes Verhältnis von Oberfläche zu Volumen haben, entstünden zwischen den Zylindern nicht nutzbare Zwischenräume. In der Ansicht von oben sähen wir Kreise und karoförmige Zwischenräume.
Daraus wird deutlich, dass es zwei Stellschrauben gibt, die wir zum Optimieren benutzen können: Zum einen suchen wir Formen, die einen möglichst geringen Umfang (bezogen auf ihre Fläche) haben und zum anderen solche, die sich so anordnen lassen, dass ihre Zwischenräume möglichst klein sind.
Im Idealfall sind die Zwischenräume zwischen den Flächen Null. In diesem Fall spricht der Mathematiker von einer Parkettierung.
Hier gibt es weitere Beispiele für Parkettierungen.
Eine Parkettierung hilft uns auch erheblich bei der anderen Optimierung durch Reduzierung des Umfangs pro umschlossene Fläche: Wenn die Fläche vollständig bedeckt ist, teilt ein Flächenelement seine Kanten immer vollständig mit seinen Nachbarn. Deswegen halbiert sich das Verhältnis von Umfang zu Fläche.
Es gibt jede Menge Interessantes zu lesen über Parkettierungen, Sechsecke und Bienenwaben. Wie eingangs erwähnt, kommt es mir auf dieser Seite auf die räumliche Vorstellung an. Deswegen soll uns folgende Behauptung erst einmal genügen:
Man kann beweisen, dass das Sechseck diejenige Form ist, die das gesuchte optimale Verhältnis liefert zwischen Kantenlänge und überdeckter Fläche.
Der Optimierungswahn geht aber noch weiter!
Wir haben uns bis hierher anschaulich überlegt, dass sechseckige Prismen die Form sind, die wir suchen. Anfangs hatten wir gesagt, dass unsere Lagerräume auf einer Seite einen Zugang und auf der anderen einen Deckel haben sollen.
Bei der Überlegung mit den Sechsecken in der Ebene ist uns aufgefallen, dass es einen erheblichen Gewinn bringt, die Kanten doppelt zu nutzen, indem wir die Sechsecke lückenlos aneinanderreihen.
Dasselbe gilt auch für den Deckel des Prismas!
Wir können den Baumaterialverbrauch pro Lagerraumvolumen weiter reduzieren, indem wir zwei Schichten von aneinandergereihten Prismen mit ihren Deckeln gegeneinander bauen. So werden auch die Deckel doppelt genutzt.
Und jetzt kommt der Clou: Eine weitere Optimierungsmöglichkeit bietet sich, wenn wir die Deckel nicht senkrecht zu den Wänden bauen sondern aus drei, jeweils leicht gekippten, rautenförmigen Teilen zusammensetzen.
Prof. Timm Grams hat das hier sehr schön beschrieben, so dass ich mir die genaue Herleitung sparen kann, denn wie schon gesagt, will ich vor allem ein Hilfsmittel zurräumlichen Vorstellung liefern.
Dieses Hilfsmittel ist ein Modell der Bienenwabe, das man aus Papier bauen kann. Um sich wirklich vorstellen zu können, wie die Waben - nun bis ins Letzte optimiert - an ihren Deckeln ineinanderpassen, braucht man mindestens vier Wabenkörper: Drei Waben aus der unteren Schicht formen den Deckel für eine Wabe aus der oberen Schicht.
Ich habe mit Geogebra das Netz einer Bienenwabe gezeichnet, das ihr drucken und ausschneiden könnt, um die Waben zu basteln:
31. März 2013, erstellt mit GeoGebra