Hemden wechseln und Fahrgemeinschaften bilden |
Die zwei folgenden Alltagsprobleme, die auf den ersten Blick gar nicht viel miteinander zu tun haben, lassen sich mit dem selben mathematischen Ansatz beschreiben, der zu einer wie ich finde überraschenden Erkenntnis führt.
Die meisten Menschen - hier schließe ich ganz dreist von mir auf andere - streben nach einem guten Wirkungsgrad, auch wenn sie das nicht immer so beschreiben würden; jeder will mit möglichst wenig Aufwand möglichst viel erreichen.
Betrachten wir den Aufwand des Hemdenbügelns: Wer seine Hemden selbst wäscht und bügelt oder dafür bezahlen muss, der könnte in die Versuchung kommen, darüber nachzudenken, wie viele Tage hintereinander er das selbe Hemd tragen kann, ohne seine Mitmenschen durch daraus resultierende Geruchsbelästigung allzu sehr zu belästigen. Je länger man ein Hemd trägt, desto weniger Hemden muss man pro Zeitraum waschen und bügeln. (Wer Hemmungen hat, solche Gedanken mit seiner Faulheit zu begründen, kann übrigens auch den Umweltaspekt in Ansatz bringen: Waschlauge belastet die Kläranlagen und Bügeln erfordert elektrische Energie.)
Das zweite Alltagsproblem ist die Frage, wie viele Mitglieder eine Fahrgemeinschaft - das häufigste Beispiel wird wohl eine für den Weg zur Arbeit sein - optimalerweise haben sollte: Nehmen wir einmal an, das Prinzip der Fahrgemeinschaft sei, dass die Mitglieder Reih' um mit Fahren an der Reihe sind und die jeweils anderen Mitglieder morgens einsammeln und abends wieder nach Hause bringen. Jedes weitere Mitglied vergrößert also den Aufwand durch Zeit und Weg für das Einsammeln. Hinzu kommt der größere Koordinierungsaufwand, wer wann mitfährt bzw. mit Fahren an der Reihe ist.
In beiden Fällen würde man spontan denken: "Je länger ich ein Hemd tragen kann, desto besser!" bzw. "Je mehr Leute mitfahren, desto besser!"
Stimmt ja prinzipiell auch, nur beinhaltet die erste Intuition außerdem - jedenfalls bei mir -, dass mit jedem weiteren Tag, den ich ein Hemd trage, bzw. mit jedem weiteren Mitfahrer, den ich zusätzlich in die Fahrgemeinschaft aufnehme, auch der Zuwachs an Nutzern immer gleich groß ist.
Genau das ist aber eben nicht so! Am schnellsten leuchtet es bei der Fahrgemeinschaft ein, weil man sich dort vorstellen kann, dass der Nutzen, den zwei Leute haben, wenn sie einen dritten in ihre Gruppe aufnehmen, geteilt werden muss.
Man kann aber auch "richtig" rechnen:
Ausgangspunkt ist:
- Ich ziehe jeden Tag ein frisches Hemd an.
- Ich fahre allein zur Arbeit.
Diesen Zustand definieren wir als Referenz: 100%
Nun führen wir die Ersparnis ein:
- Ich ziehe nur jeden zweiten Tag ein frisches Hemd an.
Ich brauche also 1/2 Hemd pro Tag. - Ich teile mir die Fahrerei zur Arbeit mit genau einem Kollegen.
Also habe ich den halben Fahraufwand.
Nun wird es spannend, wir optimieren weiter:
- Jetzt hole ich nur noch alle drei Tage ein frisches Hemd aus dem Kleiderschrank.
Die Kollegen beginnen vielleichts schon die Nase zu rümpfen, aber es geschieht schließlich im Dienste der Wissenschaft! - Außerdem erbarmen sich mein Kollege und ich und nehmen Frau Müller aus der Personalabteilung in unsere Fahrgemeinschaft mit auf.
(Aufwand-Nutzen-Überlegungen der dritten und vierten Ebene, etwa der Art, wie nett oder hübsch Frau Müller oder Kollege Maier sind oder wessen Fahrstil wir ertragen können oder nicht, lasse ich hier außen vor, weil sie nicht allgemeingültig beantwortet werden können.)
Wenden wir uns lieber der Betrachtung des Nutzens zu! Welche Ersparnis bringt uns unsere Optimierung?
- Mein Hemdenverbrauch liegt nun bei 1/3 Hemd pro Tag.
- Der Weg von und zur Arbeit, den ich mit meinem Auto und Kraftstoff bestreiten muss, beträgt 1/3 des Anfangswertes.
1/2 - 1/3 = 1/6
Der gleiche Optimierungsaufwand bringt also statt 50% Nutzen nur noch 17%!
Dass es nicht erneut 50% sein können, ist spätestens beim zweiten Nachdenken klar. Trotzdem macht man sich solche Effekte normalerweise nicht bewusst. Macht auch nichts, denn dafür gibt es ja diese Internetseite.
Da diese Seite aber unter dem Stichwort "Mathematik" steht, möchte ich das Gedankenspiel noch ein wenig weiter treiben und zu einer allgemeingültigen Lösung des Problemss kommen:
Wie groß ist der Nutzenzuwachs nach dem n-ten Optimierungsschritt?
Nennen wir den Aufwand, also die Zahl der weiteren Mitfahrer oder Tage pro Hemd, "x". Welche Abhängigkeit von x hat dann der Nutzenzuwachs? Wir suchen eine Funktionsgleichung "f(x)".
Beim ersten Optimierungsschritt, also beim Schritt von einem Hemd auf zwei bzw. von einem Fahrgemeinschaftsteilnehmer auf zwei, ist x = 1 (ein zusätzlicher Aufwand, ein Optimierungsschritt).
Letztlich ist das nur eine Definitionsfrage und wird unseren Funktionsgraphen nur eine Einheit nach links oder rechts verschieben, ob wir das erste Hemd als x = 1 bezeichnen oder das erste zusätzliche. Ich persönlich finde letztere Definition einleuchtender.
Nachfolgende Tabelle zeigt die Wertetabelle der Funktion die wir suchen:
| x | f(x) |
| 1 | 1/1 - 1/2 = 1/2 |
| 2 | 1/2 - 1/3 = 1/6 |
| 3 | 1/3 - 1/4 = 1/12 |
| 4 | 1/4 - 1/5 = 1/20 |
| ... | ... |
| n | 1/n - 1/(n+1) = 1 / (n*(n+1)) |
Wennn ich den letzten Sitzplatz in meinem Auto auffülle - angenommen es handelt sich um einen Fünfsitzer und ich habe außer mir dann vier weitere Teilnehmer der Fahrgemeinschaft - beträgt meine zusätzliche Ersparnis nur noch 5%!
In nachstehender Abbildung habe ich die Punkte der Wertetabelle in ein Koordinatensystem eingetragen.
Außerdem habe ich - frech! - auch die Funktion eingezeichnet, die der Formel in der letzten Zeile entspricht:
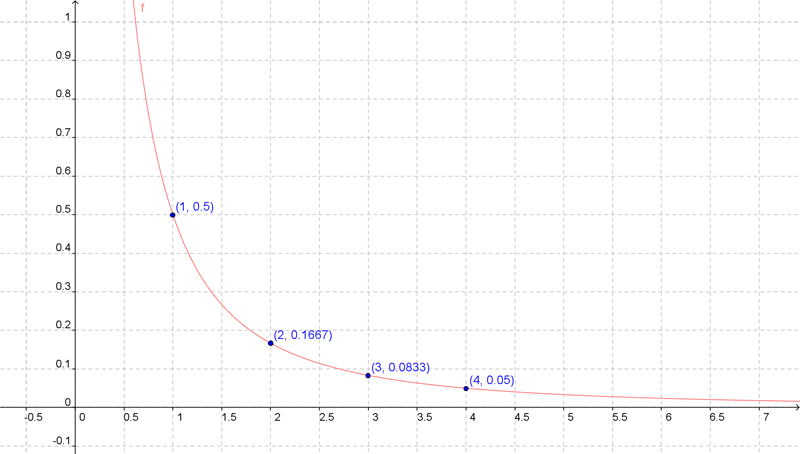
Ist das nun die Lösung unseres Problems? Ja und Nein!
Solange wir bei diskreten Werten bleiben, scheint unsere Rechenvorschrift auch für Reisebusse noch anwendbar zu sein, d.h. auch wenn ich morgens auf dem Weg zur Arbeit 41 statt 40 Kollegen einsammle, kann ich meinen Nutzengewinn damit zu 0,6 ‰ berechnen, und auch wenn ich alleine im Büro sitze und deshalb nur alle 300 Tage mein Hemd wechseln kann, stimmt der berechnete Nutzenzuwachs von 0,01 ‰. Vorstehende Grafik wirft aber neue Fragen auf:
- Stimmt das Bild mit Blick auf den Anfangswert?
- Dürfen wir so ohne weiteres eine Linie zwischen den Punkten ziehen?
- Wie groß ist der Definitionsbereich?
Die erste Frage kann - trotz vielleicht anfänglicher Verwirrung - mit "Ja!" beantwortet werden! Man könnte zunächst meinen, dass der Funktionswert f(0) = 1 sein müsste, weil wir ja eingangs gesagt haben, ein Hemd pro Tag bzw. ein Fahrer sei die 100%-Marke, aber f repräsentiert ja nicht den Aufwand selbst sondern seine Änderung, nämlich die Ersparnis durch einen weiteren Mitfahrer. Der Funktionswert f(0) sagt uns also, wie groß unsere Ersparnis ist, wenn wir statt alle Null Tage das Hemd zu wechseln eins pro Tag benutzen bzw. wenn statt keinem Fahrer einer fährt. Diese Ersparnis ist in der Tat unendlich groß, denn bei Null Tagen Tragedauer pro Hemd brauchen wir pro Tag unendlich viele, um überhaupt bekleidet zu sein.
Die Antwort auf die zweite Frage ist schon schwieriger. Natürlich kann man sich auch Zwischenwerte vorstellen: Frau Müller fährt nur jeden zweiten Tag mit oder wir schauen bei jedem Hemdenwechsel genau auf die Uhr und verfeinern unsere Skala von Tagen auf Stunden, Minuten, Sekunden oder sogar Bruchteilen davon und verlieren spätestens jetzt den Bezug zur Realität.
Wenn wir das tun, stimmt aber die Funktionsgleichung der Ersparnis nicht mehr! Aus den beiden Einsen wird der Wert, der der Optimierungsänderung entspricht, also beispielsweise 1/2, wenn Frau Müller nur jeden zweiten Tag mitfährt oder wenn wir ein Hemd 1,5 Tage lang tragen.
Durch diese Veränderung wird die Funktion steiler. An der grundsätzlichen Aussage, dass die Ersparnis mit jedem weiteren Optimierungsschritt kleiner wird, ändert sich nichts.
Bleibt die nun wirklich nur noch theoretische Frage nach dem Definitionsbereich.
Die Funktion ist außer an den Stellen 0 und -1, an denen der Nenner Null wird, über die gesamten reellen Zahlen definiert. Mir fällt aber keine sinnvolle Deutung für negative x-Werte ein.
Auch das Verhalten im Vorzeichen des Funktionswertes (zwischen -1 und 0 ist er negativ, sonst positiv) kann ich mit den urprünglich zu untersuchenden Alltagsproblemen nicht in Enklang bringen.
Macht auch nichts, das Ganze war ja ohnehin nur eine kleine, augenzwinkernde Gehirnübung!

|

|