Verhalten an den Grenzen des Definitionsbereichs bzw. im Unendlichen

Die nächste Eigenschaft, die man bei der Kurvendiskussion untersuchen kann, ist das Verhalten der Funktion, wenn das Argument - so wird die unabhängige Variable x auch genannt - unendlich groß wird bzw. wenn es sich den Grenzen des Definitionsbereichs nähert. Mit "unendlich" sind hier immer beide Enden der x-Achse gemeint: das positive und das negative Unendliche.

Das ganze ist nur eine Überlegung, nicht mehr. Man setzt für x sehr große Zahlen bzw. Zahlen in der Nähe der Grenzen des Definitionsbereichs ein und sieht sich an, was mit y passiert.

Beispiele:

• 

  Das Einführungsbeispiel f₁(x): y = (x - 1)²
  Wenn x unendlich groß wird, wird der y-Wert erst recht unendlich groß, weil das Quadrat von unendlich (die 1 spielt dann schon gar keine Rolle mehr!) unendlich mal unendlich ist.
  Geht x in Richtung minus unendlich, wird y auch unendlich und zwar positiv, weil das Quadrat einer negativen zahl immer positiv ist, selbst wenn die Zahl unendlich groß ist.
  

• Die Hyperbelfunktion
  

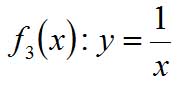
  Diese Funktion wird immer kleiner, wenn x gegen unendlich geht. y wird zwar nie ganz Null, nähert sich aber - von positiven Werten kommend - der Null immer weiter an.
  Wenn x in Richtung minus unendlich geht, passiert das selbe - aber: y ist immer negativ, wenn x negativ ist.
  Bei dieser Funktion gibt es außerdem bei null eine Lücke im Definitionsbereich. Wir müssen uns ansehen, was passiert, wenn x sich von rechts oder von links dieser Stelle annähert:
  Ist x positiv und klein, wird y positiv und sehr groß. Wenn x von rechts gegen null geht, geht y also gegen plus unendlich.
  Ist x nahe bei null und negativ, dann nimmt y betragsmäßig große negative Werte an. y geht also gegen minus unendlich, wenn x von links gegen null geht.
  

Nicht immer hat man Funktionen, die sich sofort auf eines der oben dargestellten Grundbeispiele zurückführen lassen, und es gibt auch weitere Möglichkeiten, wie sich eine Funktion im Unendlichen verhalten kann. Eine Möglichkeit ist zum Beispiel auch, dass sie sich an eine Gerade oder an eine andere Funktionsform wie eine Parabel anschmiegt.
Letzteres kommt häufig bei gebrochen rationalen Funktionen vor, also bei Funktionen bei denen man ein Polynom durch ein anderes Polynom dividiert:
Als Faustregel kann man sich merken, dass die Funktion, an die sich eine gebrochen rationale Funktion im Unendlichen anschmiegt, den Grad hat, der der Differenz "Grad des Zählerpolynoms minus Grad des Nennerpolynoms" entspricht. Haben Zähler und Nenner also den gleichen Grad, wird die Funktion sich im Unendlichen an eine Horizontale anschmiegen, ist der größte x-Exponent im Zähler um 1 größer als im Nenner, wird die Asymptote eine Gerade sein, ist er um 2 größer eine Parabel usw.
Wie man solche Asymptoten berechnet, ist bei serlo.org sehr gut beschrieben! Auch wie man dafür die Polynomdivision durchführt.
Manchmal muss man auch einen "Trick" anwenden, um einen Grenzwert herauszubekommen. Der wichtigste ist die Regel von l'Hospital, die hier sehr gut erklärt ist. Auch hier bei studyflix.de.