Stetigkeit und Differenzierbarkeit

Was ist das nun wieder?

Eigentlich sind Stetigkeit und Differenzierbarkeit zwei Eigenschaften, die man gleich zu Beginn der Kurvendiskussion prüft. Ich behandele sie deshalb erst hier, weil die Gedanken auf den vorangegangenen Seiten wichtig sind, um zu verstehen, warum diese Dinge Voraussetzungen sind.

Stetigkeit

Anschaulich gesprochen ist Stetigkeit die Eigenschaft einer Funktion, dass sie keine Sprünge macht.
Nachfolgend gezeigte Funktion ist also nicht stetig, jedenfalls nicht überall. An der Stelle x = 2 hat sie einen Sprung.

Es ist anschaulich leicht einzusehen, dass man für solche Sprungstellen keine Tangentensteigung finden kann; welche sollte man auch nehmen? Die Steigung, mit der der linke Ast aufhört oder doch lieber die, mit der der rechte Ast weiter geht? Oder vielleicht doch lieber die Verbindungslinie der beiden Äste? Aber die ist senkrecht, die Steigung (der Differenzenquotient) also nicht definiert bzw. unendlich.

Die mathematische Definition der Stetigkeit ist etwas trickreicher; sie lautet:
Die Funktion f ist stetig an einer Stelle x₀, wenn zu jedem ε > 0 ein δ > 0 existiert, so dass
für alle x mit | x - x₀ | < δ gilt: | f(x) - f(x-x₀) | < ε

Ich finde, es genügt, sich zu merken, dass eine Funktion, deren Graph keine Sprünge macht, stetig ist.

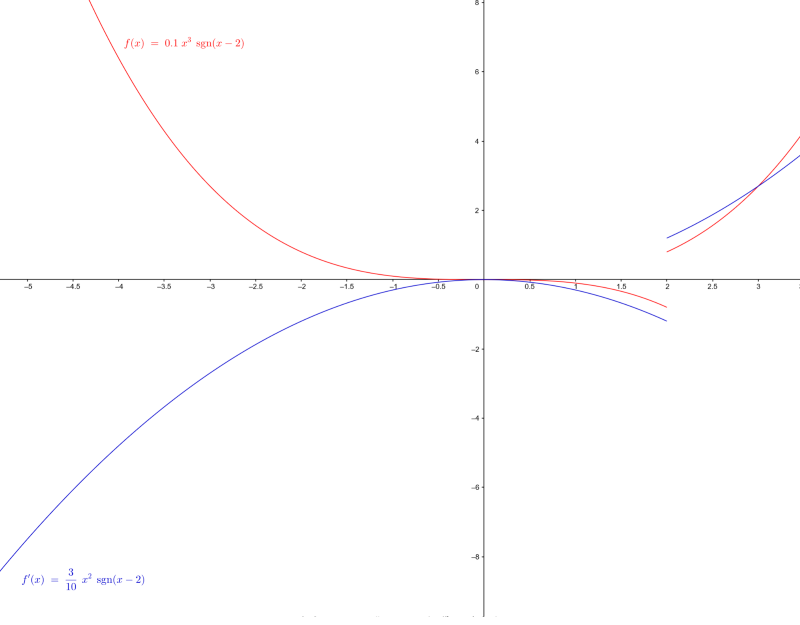
Vorstehendes Bild zeigt zwei Funktionen, die nicht stetig sind, weil sie an der Stelle x=2 Sprünge machen.

Differenzierbarkeit

Man kann sich noch eine weitere Möglichkeit vorstellen, bei der die Funktion zwar nicht springt, man aber für bestimmte Punkte trotzdem keine Tangentensteigung ausrechnen kann: Wenn der Funktionsverlauf einen Knick hat.

In nachfolgendem Bild lässt sich die Steigung der Tangente mit dem Schieberegler einstellen. Gibt es einen Wert, von dem man sagen könnte, das sei die Steigung der Funktion an der Stelle x = π ? Probier es aus!

Die Antwortet lautet: Nein. Deswegen ist die Funktion an der Knickstelle nicht differenzierbar.
Mathematisch exakt formuliert ist eine Funktion an einer Stelle x₀ genau dann differenzierbar, wenn der Grenzwert des Differenzenquotienten, mit dem man die Tangentensteigung berechnet, existiert.

Wenn eine Funktion differenzierbar ist, so ist sie auch stetig, aber eine stetige Funktion muss nicht notwendigerweise auch differenzierbar sein.

Beispiel:
Die Wurzelfunktion hat an der Stelle x₀ = 0 eine senkrechte Tangente, sie ist dort also nicht differenzierbar. Trotzdem ist sie an dieser Stelle immer noch stetig. Ebenso die Betragsfunktion: Sie ist an der Stelle Null stetig aber nicht differenzierbar (sie macht dort einen Knick).