| |
Schein und Sein in der Mathematik |
Wahrscheinlichkeit und Wahrscheinlichkeitsverteilung
"Wahrscheinlichkeiten kann man nur berechnen, wenn man die Wahrscheinlichkeitsverteilung kennt!"
Dieser Satz - so widersinnig er sich zunächst anhören mag - hat bei mir den Knoten gelöst, den ich seit der Schulzeit in Sachen Wahrscheinlichkeitsrechnung im Kopf hatte. Wahrscheinlichkeitsrechnung widerspricht häufig der Intuition. Das macht sie einerseits schwer verständlich, andererseits sollte man sich genau deswegen mit ihren Grundzügen ein wenig auskennen, um nicht wissentlich oder unwissentlich falsch vorgetragenen statistischen Argumenten ausgeliefert zu sein.
An anderer Stelle habe ich schon gezeigt, wie irreführend Prozentangaben verwendet werden können.
Auf dieser Seite will ich die Aussagekraft statistischer Argumente beleuchten, bei denen ja auch häufig Prozentwerte verwendet werden. Dazu zählen beispielhaft ein positiver Test auf eine seltene Krankheit, ein Fernsehbericht über Bio-Äpfel und ein politisches Argument über den Zusammenhang von sozialer Herkunft und Bildung.
Aber der Reihe nach:
Wenn ich wissen will, wie groß die Wahrscheinlichkeit ist, aus einer Urne eine rote Kugel zu ziehen, dann muss ich zwei Dinge wissen:
- Wie viele rote Kugeln sich in der Urne befinden.
- Wie viele Kugeln sich insgesamt in der Urne befinden.
Genau diese Information ist die Wahrscheinlichkeitsverteilung!
Die gesuchte Wahrscheinlichkeit ist dann einfach das Verhältnis (der Quotient) der beiden Zahlen a/b.
Warum Statistiker ihre verschiedenfarbigen Kugeln ausgerechnet in Urnen aufbewahren statt in Dosen oder Kisten, konnte mir bisher übrigens noch niemand erklären. Vielleicht hängt das damit zusammen, dass dieses Wort am besten suggeriert, dass man beim Ziehen der Kugel natürlich nicht hinsehen darf, damit es ein Zufallsexperiment bleibt.
Genauso dürfen die Kugeln auch anders nicht zu unterscheiden sein, sie müssen gut gemischt sein usw., damit die mathematisch wichtige Nebenbedingung erfüllt wird, dass jede Kugel mit der gleichen Wahrscheinlichkeit gezogen wird.
Ein solches Experiment, bei dem die Elementar-Ereignisse (hier: das Ziehen einer Kugel) alle gleich wahrscheinlich sind, nennt man übrigens Laplace-Experiment.
Das Urnenmodell ist auch deshalb so beliebt, weil sich viele Statistik-Aufgaben darauf zurückführen lassen. Unten ist dazu ein einfaches Beispiel angegeben.
Einführungsbeispiel:
Berechnen Sie die Wahrscheinlichkeit, dass sich unter zwei Kugeln, die Sie nacheinander aus einer Urne ziehen, genau eine blaue befindet!
Viele Menschen neigen dazu, eine Wahrscheinlichkeit anzugeben. Die meisten antworten: "50 %"
Diese Aufgabe ist aber so gar nicht zu lösen! Warum nicht? Weil die Wahrscheinlichkeitsverteilung nicht angegeben ist, also wie viele blaue Kugeln sich überhaupt in der Urne befinden und wie viele Kugeln es insgesamt sind. Je nachdem, wie diese Verteilung ist, kann die Wahrscheinlichkeit zwischen 0% (es befindet sich gar keine blaue Kugel in der Urne) und 100% (es befinden sich ausschließlich blaue Kugeln in der Urne) schwanken.
Und nein: Auch wenn 50% genau zwischen 0% und 100% liegt, ist es trotzdem keine gültige Antwort!
Aber fangen wir vorne an:
In einer Urne sollen sich drei rote, zwei gelbe und fünf blaue Kugeln befinden, insgesamt also zehn Stück.
Die Wahrscheinlichkeit, eine rote Kugel zu ziehen beträgt dann p(rot) = 3/10 = 30 %
Das ist das Verhältnis der Anzahl der roten Kugeln und der Gesamtzahl der Kugeln.
Als Formelzeichen für Wahrscheinlichkeiten verwendet man p wie probability (engl. Wahrscheinlichkeit). In Klammern dahinter steht, auf welches Ereignis sich der angegebene Wert bezieht, hier: eine rote Kugel zu ziehen.
Aus dem Urnenmodell wird auch schnell klar, dass die Wahrscheinlichkeit, beim zweiten Ziehen eine blaue Kugel zu erwischen, davon abhängt, ob man die zuerst gezogene Kugel zurücklegt oder nicht und wenn nicht, welche Farbe die zuerst gezogene Kugel hatte. Das liegt daran, dass sich die oben beschriebenen Parameter a) und b) der Wahrscheinlichkeitsverteilung ändern, wenn wir die erste Kugel nicht zurücklegen.
Ein Beispiel für die Anwendung des Urnenmodells auf ein anderes Zufallsexperiment geht so:
Wie groß ist die Wahrscheinlichkeit, beim Werfen eines Würfels eine fünf zu würfeln?
In der Urne sind sechs von eins bis sechs durchnummerierte Kugeln. (Das ist die Wahrscheinlichkeitsverteilung!)
Wir ziehen eine Kugel. p(5) = 1/6 weil es eine Kugel von sechs gibt, die das gewünschte Ergebnis liefert.
Wieder setzen wir gedanklich bei der Wahrscheinlichkeitsverteilung voraus, dass es sich um ein Laplace-Experiment handelt, der Würfel also fair ist und alle Ereignisse gleich wahrscheinlich sind.
So weit, so einfach.
Was passsiert, wenn man Experimente betrachtet, bei denen nacheinander unterschiedlich wahrscheinliche Teilereignisse passieren sollen?
Als Beispiel kann wieder unsere Urne von oben dienen, in der sich drei rote, zwei gelbe und fünf blaue Kugeln befinden.
Wir ziehen drei Mal ohne Zurücklegen. Wie groß ist die Wahrscheinlichkeit, dass alle drei gezogenen Kugeln rot sind?
Um bei solchen Experimenten den Überblick zu behalten, zeichnet man sich am besten einen Baum, in dem alle möglichen Verläufe des Experiments dargestellt sind:
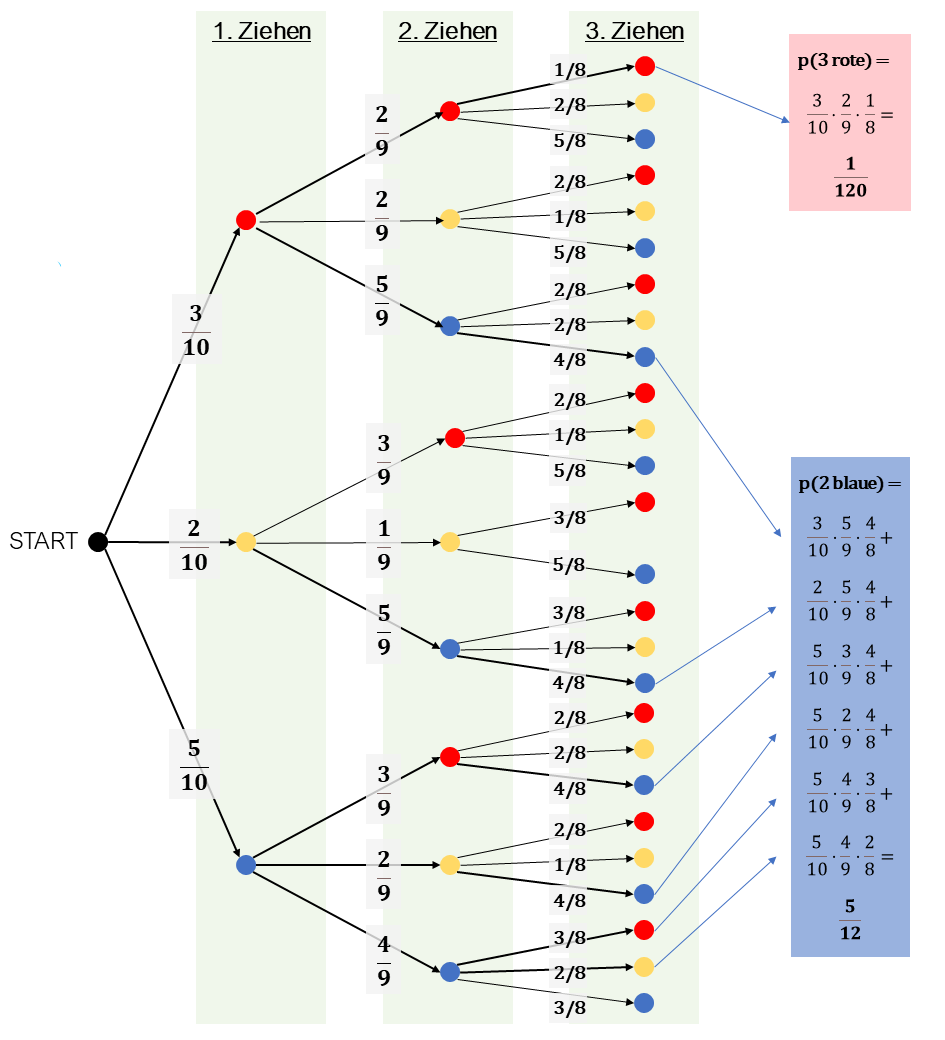 Ausgehend von einem Startpunkt (links im Bild) zeichnet man einen Pfeil zu jedem möglichen Ergebnis des ersten Teilexperiments. In unserem Beispiel gibt es die drei Möglichkeiten, eine rote, eine gelbe oder eine blaue Kugel zu ziehen.
Ausgehend von einem Startpunkt (links im Bild) zeichnet man einen Pfeil zu jedem möglichen Ergebnis des ersten Teilexperiments. In unserem Beispiel gibt es die drei Möglichkeiten, eine rote, eine gelbe oder eine blaue Kugel zu ziehen.
An jeden dieser Pfeile schreibt man die Wahrscheinlichkeit, dass dieses Teilereignis eintritt. Beim Urnenmodell ist das jeweils die Anzahl Kugeln der entsprechenden Farbe, die sich in der Urne befinden, geteilt durch die Gesamtzahl Kugeln in der Urne. Wenn wir alle Ereignisse und Wahrscheinlichkeiten richtig aufgeschrieben haben, muss die Summe aller Wahrscheinlichkeiten 1 ergeben.
An unserem Beispiel kann man übrigens sehr schön sehen, dass sich das Urnenmodell auch dann zur Berechnung von Wahrscheinlichkeiten eignet, wenn die Ereignisse (hier: rot, gelb, blau) unterschiedlich wahrscheinlich sind, die Wahrscheinlichkeitsverteilung also keine Gleichverteilung ist. Das obwohl wir für jede einzelne Kugel die gleiche Wahrscheinlichkeit, gezogen zu werden, vorausgesetzt haben.
Mit dem zweiten und allen weiteren Teilereignissen verfährt man analog: Von jedem möglichen Ergebnis ausgehend überlegt man sich, welche Möglichkeiten es für den Ausgang des nächsten Teilexperiments gibt und wie wahrscheinlilch sie sind. Jede Möglichkeit bekommt einen neuen Ast im Ereignisbaum.
Zu beachten ist hier, dass es einen Unterschied macht, ob die im ersten Teilexperiment gezogene Kugel zurückgelegt wird oder nicht. Denn wenn sie wie in unserem Beispiel nicht zurückgelegt wird, ändert sich ja die Anzahl Kugeln, die sich noch in der Urne befinden - und zwar sowohl die Gesamtzahl (Nenner der Wahrscheinlichkeit) als auch die Anzahl der Kugeln der zuvor gezogenen Farbe (ggf. Zähler der Wahrscheinlichkeit)! Im Extremfall ändert sich sogar die Anzahl der möglichen Ereignisse, wenn nämlich von einer Farbe alle Kugel gezogen worden sind. In unserem Beispiel sieht man das bei der 3. Ziehung, bei der es in einem Fall keine gelben Kugeln mehr gibt (in der Mitte des Ereignisbaums zu sehen).
Auch bei der zweiten und allen weiteren Ziehungen müssen sich alle Wahrscheinlichkeiten zu 1 aufaddieren.
Jeder Weg von links nach rechts durch den Baum mündet sozusagen in einem Blatt, das einen möglichen Ausgang des Gesamt-Zufallsexperiments darstellt.
Wie groß ist nun die Wahrscheinlichkeit, dass alle drei gezogenen Kugeln rot sind?
Wir sehen, dass dieses Ergebnis durch den obersten Ast des Baumes dargestellt wird. An jedem Zweig steht eine Wahrscheinlichkeit dafür, dass dieser Weg im Experiment beschritten wird. Für das Endergebnis müssen wir diese Wahrscheinlichkeiten multiplizieren, denn jeder Ast repräsentiert ja den Anteil der Möglichkeiten am Ausgang des Ergebnisses.
In diesem Beispiel ist also die Wahrscheinlichkeit, nur rote Kugeln zu ziehen: p(3 rote) = 1/120 = 0,833 %, also recht klein.
Wie groß ist die Wahrscheinlichkeit, genau zwei blaue Kugeln zu ziehen?
Dafür müssen wir den Pfad suchen, auf dem wir zwei blaue Kugeln erhalten. Aber HALT! Davon gibt es mehrere!
In einem solchen Fall müssen wir die Wahrscheinlichkeiten für jeden Verlauf addieren. Im Beispiel kommen wir somit auf: p(2 blaue) = 5/12 = 41,7 % (vgl. blauer Kasten im Bild!).
Dieses Ereignis verdeutlicht auch, dass man auf exakte Formulierung achten muss: "genau zwei" bedeutet "zwei und nicht drei".
Wenn wir das Ereignis, das durch den untersten Ast des Baumes repräsentiert wird, einschließen wollten, müssten wir "mindestens zwei blaue" sagen.
Ein solcher Ereignisbaum stellt alle möglichen Verläufe eines Experimentes dar. Man sieht schon an diesem relativ einfachen Beispiel, dass dieses Vorgehen Grenzen der Machbarkeit hat, weil die Zahl der Möglichkeiten in der Regel sehr schnell ansteigt. Um zum Beispiel alle möglichen Verläufe einer Lottoziehung 6 aus 49 darzustellen, müsste man 10.068.347.520 Äste darstellen!
In solchen Fällen muss man etwas mehr nachdenken und kann weniger veranschaulichen:
Um die Wahrscheinlichkeit zu berechnen, sechs Richtige zu tippen, müssen wir wieder die Anzahl der "günstigen" Möglichkeiten durch die Gesamtzahl der Möglichkeiten teilen:
"Günstig" bedeutet in diesem Fall, dass die sechs Zahlen auf unserem Tippzettel die gleichen sind wie die Gezogenen. Dabei spielt die Reihenfolge der Ziehung keine Rolle.
Deswegen gibt es nicht nur eine günstige Möglichkeit sondern die Anzahl der günstigen Möglichkeiten ist die Anzahl der möglichen Vertauschungen (man sagt auch "Permutationen") derselben sechs Zahlen. Um diese zu berechnen, stellt man sich am besten ein weiteres Urnenmodell vor: In der Urne befinden sich genau die sechs Kugeln, auf denen dieselben Zahlen stehen, wie auf unserem Tippzettel. Die Ziehung ohne Zurücklegen läuft dann wie folgt ab:
Bei der ersten gezogenen Kugel gibt es sechs Möglichkeiten, dass eine Richtige gezogen wird, nämlich eine der sechs Zahlen auf unserem Tippzettel.
Bei der zweiten Ziehung sind noch fünf Richtige übrig, bei der dritten vier usw.
Deswegen gibt es insgesamt 6 · 5 · 4 · 3 · 2 · 1 = 720 Möglichkeiten.
Diese Folge von Multiplikationen nennt man auch Fakultät und schreibt sie mit einem Ausrufungszeichen: 6! = 720
Auf ähnliche Weise kann man sich überlegen, wie viele Möglichkeiten n es insgesamt für das Ziehen von sechs aus 49 Kugeln gibt:
Bei der ersten Ziehung gibt es 49 Möglichkeiten, bei der zweiten noch 48 usw. bis bei der letzten Ziehung noch 44 Kugeln in der Trommel sind.
Deswegen ist n = 49 · 48 · 47 · 46 · 45 · 44 = 49! / (49 - 6)! = 10.068.347.520 die oben schon genannte Zahl.
Die Wahrscheinlichkeit für sechs Richtige ist also: p(6 Richtige) = 720 / 10.068.347.520 = 1 / 13.983.816 also sehr klein!
Bedingte Wahrscheinlichkeiten
Die Quintessenz bis hierher:
Man berechnet eine Wahrscheinlichkteit aus der Wahrscheinlichkeitsverteilung, indem man die Anzahl der (gleich wahrscheinlichen oder mit ihrer Wahrscheinlichkeit gewichteten) Möglichkeiten, in einem Experiment das gewünschte Ergebnis zu erzielen (dasjenige für welches man die Wahrscheinlichkeit berechnen will), durch die Gesamtzahl der Möglichkeiten teilt.
Das ähnelt nicht nur zufällig der Prozentrechnung! Und wir erinnern uns, dass die wichtigste Frage bei der Prozentrechung diejenige nach der Grundgesamtheit und möglicher Änderungen daran ist.
Stellen wir uns das folgende Szenario vor:
Krankheitsdiagnose
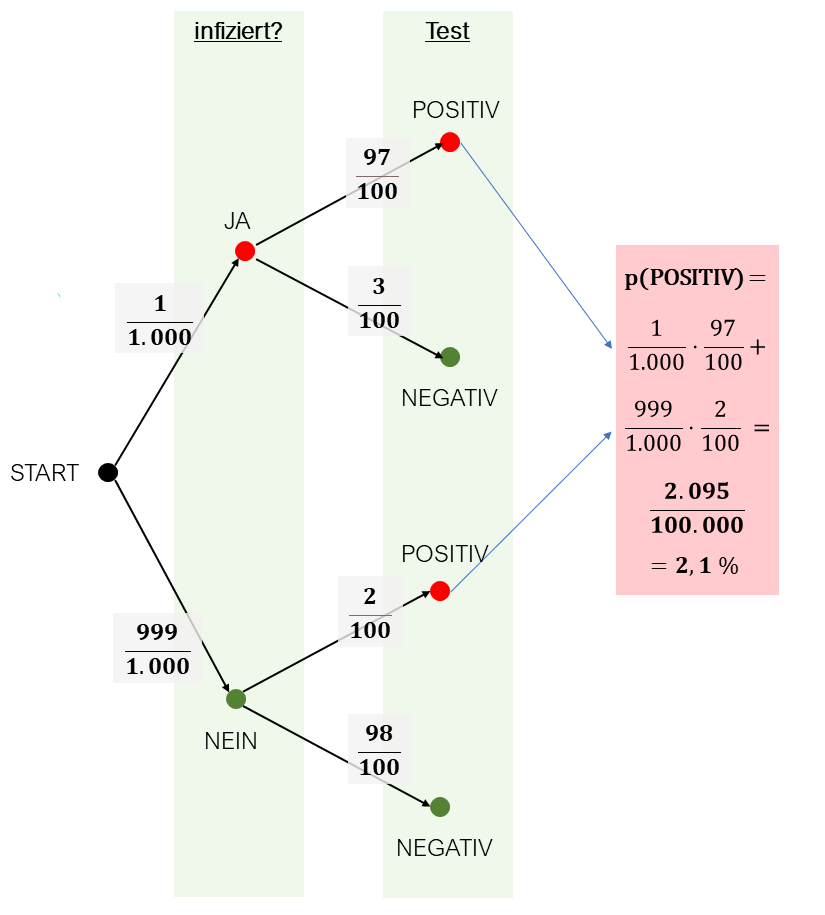 Ein Promille der Menschen leide an einer Krankheit, die erst einige Zeit nach der Infektion ausbreche und dann schwere Folgen habe. Sie sei nur heilbar, wenn sie vor dem Ausbruch diagnostiziert werde. Während der Inkubationszeit (der Zeit zwischen Infektion und Ausbruch) sei sie ohne Symptome und könne nur mit einem Test festgestellt werden. Dieser Test habe eine Sensitivität von 97 %. Das bedeutet, dass der Test in 97 % der Fälle bei einer tatsächlich infizierten Person ein positives Ergebnis liefert. Mit einer gewissen Wahrscheinlichkeit - in diesem Beispiel wollen wir 2 % annehmen - liefere der Test aber auch dann ein positives Ergebnis, wenn die getestete Person nicht infiziert ist. Man könnte das die Falschalarmrate nennen, Mediziner sprechen statt dessen aber lieber von einer Spezifität von 98 %.
Ein Promille der Menschen leide an einer Krankheit, die erst einige Zeit nach der Infektion ausbreche und dann schwere Folgen habe. Sie sei nur heilbar, wenn sie vor dem Ausbruch diagnostiziert werde. Während der Inkubationszeit (der Zeit zwischen Infektion und Ausbruch) sei sie ohne Symptome und könne nur mit einem Test festgestellt werden. Dieser Test habe eine Sensitivität von 97 %. Das bedeutet, dass der Test in 97 % der Fälle bei einer tatsächlich infizierten Person ein positives Ergebnis liefert. Mit einer gewissen Wahrscheinlichkeit - in diesem Beispiel wollen wir 2 % annehmen - liefere der Test aber auch dann ein positives Ergebnis, wenn die getestete Person nicht infiziert ist. Man könnte das die Falschalarmrate nennen, Mediziner sprechen statt dessen aber lieber von einer Spezifität von 98 %.
Verständlicherweise möchten wir gerne wissen, ob wir mit dieser Krankheit infiziert sind. Wir machen also den beschriebenen Test. Das Ergebnis ist positiv! Wie groß ist die Wahrscheinlichkeit, tatsächlich infiziert zu sein, wenn der Test positiv ist?
Glücklicherweise kennen wir in diesem Beispiel die Wahrscheinlichkeitsverteilung! Deswegen können wir die Wahrscheinlichkeit ausrechnen:
Das tun wir zunächst mit einem Ereignisbaum, der sich ja oben schon bewährt hat.
Darin berechnen wir zunächst wie zuvor beschrieben für jeden Zweig, der mit einem positiven Testergebnis endet, seine Wahrscheinlichkeit und addieren sie. Damit kommen wir auf etwas mehr als 2 % Wahrscheinlichkeit für ein positives Testergebnis! Das ist schon mal überraschend, da doch nur jeder Tausendste infiziert ist!
Wenn wir uns die Berechnung ansehen, stellen wir fest, dass der größte Anteil der Möglichkeiten, ein positives Testergebnis zu erhalten, aus den Falschalarmen im unteren Zweig kommen. Ca. 95 % der positiven Testergebnisse sind Falschalarme! Die Wahrscheinlichkeit, tatsächlich infiziert zu sein, beträgt also trotz des positiven Testergebnisses nur ungefähr 5 %!
Um diesen Sachverhalt besser zu veranschaulichen und die eigentlich interessierende bedingte Wahrscheinlichkeit zu berechnen, hat sich die sogenannte Vierfeldertafel durchgesetzt. Tatsächlich hat sie viel mehr Felder, aber die vier in der Mitte sind die entscheidenden:
|
infiziert |
SUMME |
| JA |
NEIN |
Test |
positiv |
97 |
1.998 |
2.095 |
| negativ |
3 |
97.902 |
97.905 |
| SUMME |
100 |
99.900 |
100.000 |
Vierfeldertafel Nr. 1:
1 ‰ Infizierte in der Grundgesamtheit, Sensitivität: 97 %, Spezifität: 98 % |
Eine Vierfeldertafel besteht aus je zwei Zeilen bzw. Spalten für die beiden Ereignisse, die untersucht werden. Hier ist das eine Ereignis die Infektion und das andere das Testergebnis. Rundherum gibt es Beschriftungen (oben und links) bzw. Tabellenzellen für die jeweiligen Summen (rechts und unten).
Für das oben beschriebene Beispiel sieht die Vierfeldertafel so aus, wie rechts zu sehen (Vierfeldertafel Nr. 1), wenn wir annehmen, dass die Grundgesamtheit der betrachteten Personen 100.000 beträgt. Da wir am Ende nur relative Werte betrachten, können wir diese Zahl willkürlich wählen.
Von diesen 100.000 Personen sind 1 ‰, also 100 Personen mit der Krankheit infiziert. Diese Zahl steht in der Zeile "SUMME" in der Spalte der Infizierten.
Wegen der Sensitivität des Tests von 97 % fällt bei 97 dieser 100 Personen der Test positiv aus. Bei dreien bleibt er trotz Infektion negativ. Diese beiden Zahlen stehen in den entsprechenden Zeilen der Testergebnisse in der Spalte der Infizierten.
Wegen der Spezifität des Tests von 98 % werden von den 99.900 nicht infizierten Personen 97.902 richtig negativ getestet.
2 % der Gesunden erhalten aber ebenfalls ein positives Testergebnis. Das sind 1.998 Personen.
Diese beiden Zahlen stehen in der Spalte der Gesunden in den jeweiligen Zeilen der Testergebnisse.
Nun können wir die Wahrscheinlichkeit, tatsächlich infiziert zu sein, wenn wir ein positives Testergebnis haben, wie folgt ausrechnen:
Mit dem positiven Testergebnis sind wir eine von 2.095 Personen. Von diesen sind 97 infiziert und 1.998 sind gesund (vgl. Vierfeldertafel Nr. 2!).
Im Urnenmodell könnte man das so formulieren, dass sich in einer Urne 2.095 Kugeln befinden, wovon 97 rot und 1.998 grün sind.
Wenn man daraus eine Kugel zieht, ist die Wahrscheinlichkeit, dass die Kugel rot (die Person infiziert) ist: p(rot) = 97 / 2.095 = 4,63 %
Mit anderen Worten: Ein positives Testergebnis ist überhaupt noch kein Anlass zur Sorge!
Aber welche Aussagekraft hat der Test dann?
Und was muss man tun, um eine Infektion nun wirklich eindeutig zu diagnostizieren?
Dafür gibt es eine einfache Möglichkeit: Man muss einen zweiten Test machen!
Das leuchtet auf den ersten Blick nicht unbedingt ein, denn was soll bei einem zweiten Test anders sein als bei einem ersten?! Die Antwort ist: Die Wahrscheinlichkeitsverteilung! Die Grundgesamtheit beim zweiten Test enthält nicht mehr 1 ‰ Infizierte sondern 4,63 %. In der Vierfeldertafel rutscht damit die Zeile mit den positiven Testergebnissen in die Summenzeile. Im Ganzen sieht das dann so aus:
|
infiziert |
SUMME |
| JA |
NEIN |
Test |
positiv |
94,09 |
39,96 |
134,05 |
| negativ |
2,91 |
1.958,04 |
1.960,95 |
| SUMME |
97 |
1.998 |
2.095 |
Vierfeldertafel Nr. 2:
4,63 % Infizierte in der Grundgesamtheit, Sensitivität: 97 %, Spezifität: 98 % |
Ist auch der zweite Test positiv, dann haben wir schon eine Wahrscheinlichkeit, tatsächlich infiziert zu sein, von p(infiziert) = 94,09 / 134,05 = 70,2 %
Wem diese Aussagekraft immer noch nicht genügt, der kann einen dritten Test machen, der dann eine Sicherheit von 99,1 % hat, wenn er auch positiv ist.
An den Kommazahlen in der Vierfeldertafel müssen wir uns nicht stören. Wir haben bisher wegen der besseren Anschaulichkeit zwar immer mit absoluten Personenzahlen gerechnet, die nur natürliche Zahlen sein können, aber man kann eine Vierfeldertafel genausogut mit Prozentwerten befüllen. Die Dezimalzahlen können bei den Divisionsrechnungen auftreten.
Woher kommt diese anfängliche Unzuverlässigkeit des ersten Testergebnisses?
Daher dass die Krankheit nur relativ selten auftritt!
Dadurch fallen beim ersten Test die vielen falsch positiven Ergebnissse so sehr ins Gewicht.
Diese ganze Rechnerei ging natürlich von idealen Bedingungen aus, insbesondere davon, dass wir die Wahrscheinlichkeitsverteilung - also die Verbreitung der Krankheit, die Sensitivität und die Spezifität - kennen. Das ist im echten Leben nicht immer der Fall! Mein Ziel ist, mit diesen Rechnungen zu zeigen, was eine Wahrscheinlichkeit uns sagen kann und vor allem, was sie uns nicht sagen kann!
Das führt mich zu zwei weiteren Beispielen aus ganz anderen Lebensbereichen, bei denen die Rechnung aber den gleichen Prinzipien folgt. Sie sollen zeigen, wie wenig aussagekräftig die Angabe von Wahrscheinlichkeiten - oder besser: von relativen Häufigkeiten - sein kann. (Die Wahrscheinlichkeit ist der Grenzwert der relativen Häufigkeit für unendlich viele Versuche.)
Bio-Äpfel
In der Sendung Nelson Müllers Lebensmittelreport - Wie gut sind Äpfel, Orangensaft und Bio-Bananen? (Sendeung vom 14.01.2020, Video verfügbar bis 13.01.2025) wird zwischen Minute 5:17 und 5:40 eine Studie des Niedersächsischen Landesamtes für Verbraucherschutz zitiert, allerdings unvollständig, so dass die erwünschte Aussage verloren geht und - schlimmer noch - man intuitiv zu einer falschen Schlussfolgerung gelangen kann.
Es wird zitiert, dass im Jahr 2018 an 91 Äpfeln eine Untersuchung auf Pestizidrückstände durchgeführt wurde.
Von den 8 gefundenen unbelasteten Äpfeln seien 7 aus biologischem Anbau gewesen, nur 1 aus konventionellem Anbau habe keine Rückstände aufgewiesen.
|
Anbauart |
SUMME |
| biologisch |
konventionell |
| Pestizidrückstände |
ja |
|
|
83 |
| nein |
7 |
1 |
8 |
| SUMME |
|
|
91 |
| Vierfeldertafel Nr. 3: Angaben aus dem Zitat |
Wenn man diese Angaben und diejenigen, die man daraus errechnen kann, in eine Vierfeldertafel einträgt, wie wir sie oben kennengelernt haben, sieht das so aus wie nebenstehend in Vierfeldertafel Nr. 3 gezeigt.
In dem Beitrag sollte ausgesagt werden, dass Bio-Äpfel im Gegensatz zu solchen aus konventionellem Anbau nicht mit Pestizidrückständen belastet sind.
Mathematisch ausgedrückt: Es soll gezeigt werden, dass die Wahrscheinlichkeit, auf einem Apfel aus biologischem Anbau Pestizid-Rückstände zu finden, gleich Null ist.
Wie oben gezeigt benötigen wir zur Berechnung dieser Wahrscheinlichkeit die Wahrscheinlichkeitsverteilung, mit anderen Worten: die fehlenden Angaben in der unteren Summenzeile.
Komischerweise neigen Menschen dazu, auch ohne Kenntnis der Wahrscheinlichkeitsverteilung aus solch unvollständigen Daten eine Schlussfolgerung zu ziehen. Alle Personen aus meinem Umfeld, die ich mit dieser Frage genervt habe, waren ohne Zögern bereit, diese Daten als Beleg dafür zu akzeptieren, dass Bio-Äpfel nicht mit Pestiziden belastet sind.
|
Anbauart |
SUMME |
| biologisch |
konventionell |
| Pestizidrückstände |
ja |
83 |
0 |
83 |
| nein |
7 |
1 |
8 |
| SUMME |
90 |
1 |
91 |
Vierfeldertafel Nr. 4:
Erste mögliche Interpretation der Apfeldaten
blau: angegebene Daten
rot: zu den gegebenen Daten willkürlich aber schlüssig ergänzte Daten
|
Auch die nebenstehende, mit den gegebenen Daten mögliche Berechnung in Vierfeldertafel Nr. 4, konnte daran nichts ändern:
Sie zeigt, dass die angegebenen Daten (blaue Felder) sogar dann richtig wären, wenn ausschließlich Bio-Äpfel pestizidverseucht wären, wenn die Wahrheit also genau das Gegenteil von dem wäre, was der durchschnittliche Zuschauer intuitiv aus ihnen abliest!
Wenn die Verteilung in der Grundgesamtheit so war, dass nur 1 Apfel aus konventionellem Anbau stammte, dann wäre die Wahrscheinlichkeit, dass Äpfel aus konventionellem Anbau sauber sind,
p(konventionell sauber) = 100 %!
Die Wahrscheinlichkeit, dass Äpfel aus biologischem Anbau sauber sind, wäre dann
p(biologisch sauber) = 7/90 = 7,8 % - sehr wenig!
Das ist eine mit den gegebenen Daten gültige Interpretation, wenngleich die Untersuchung von nur einem Apfel aus konventionellem Anbau natürlich wenig aussagekräftig wäre.
|
Anbauart |
SUMME |
| biologisch |
konventionell |
| Pestizidrückstände |
ja |
38 |
45 |
83 |
| nein |
7 |
1 |
8 |
| SUMME |
45 |
46 |
91 |
Vierfeldertafel Nr. 5:
Zweite, "vernünftigere" Interpretation der Apfeldaten
blau: angegebene Daten
rot: zu den gegebenen Daten willkürlich aber schlüssig ergänzte Daten
|
Nehmen wir also eine "vernünftigere" Aufteilung der Äpfel in der Grundgesamtheit auf die verschiedenen Anbauarten an! Wenn ich eine solche Untersuchung machen sollte, würde ich die beiden Gruppen ungefähr gleich groß machen. Das ist in Vierfeldertafel Nr. 5 gezeigt.
Wenn die Verteilung in der Grundgesamtheit so war, dass 46 Äpfel aus konventionellem Anbau stammten, dann wäre die Wahrscheinlichkeit, dass Äpfel aus konventionellem Anbau sauber sind,
p(konventionell sauber) = 1/46 = 2,2 %!
Die Wahrscheinlichkeit, dass Äpfel aus biologischem Anbau sauber sind, wäre dann
p(biologisch sauber) = 38/45 = 84,4 % - also schon deutlich besser, aber immer noch schlechter, als man erwarten würde und vor allem schlechter als der Beitrag aussagen wollte.
Schon an diesen stark unterschiedlichen Interpretationsmöglichkeiten sieht man, wie wenig - nämlich überhaupt nicht - aussagekräftig die im ZDF-Beitrag angegebenen Informationen sind. Wenn man überhaupt eine Aussage daraus ableiten kann, dann die, dass in fast jedem denkbaren Fall auch Äpfel aus biologischem Anbau Pestizid-Rückstände aufweisen können. Trotzdem nimmt die - zugegebenermaßen nicht repräsentative - Stichprobe von Testpersonen die Daten als Beleg für die Qualität von Bio-Äpfeln. Nun, wenn die Leute dadurch dazu gebracht werden, grundsätzlich jeden Apfel vor dem Verzehr abzuwaschen, ist ja immerhin etwas erreicht, wenngleich auch das nicht gegen Pestizid-Rückstände helfen soll.
Mir persönlich wäre zudem wichtiger, dass sich eine etwas kritischere Auseinandersetzung mit vermeintlich stichhaltigen Belegen durchsetzt.
Im vorliegenden Fall sollte nicht vorsätzlich getäuscht werden. Das ergibt sich aus dem Rest des Beitrages, der deutlich pro Bio-Obst ist.
Trotzdem wäre ich als mathematisch interessierter Bio-Obstbauer (gibt es so etwas?) ganz schön sauer! Denn durch das Unterschlagen einer einzigen Zahl wird das Bio-Obst zunächst schlechter gemacht, als es in Wirklichkeit ist! In der Originalstudie des Niedersächsischen Landesamtes für Verbraucherschutz kann man nämlich nachlesen, dass von den 91 getesteten Äpfeln 7 aus biologischem Anbau stammten.
|
Anbauart |
SUMME |
| biologisch |
konventionell |
| Pestizidrückstände |
ja |
0 |
83 |
83 |
| nein |
7 |
1 |
8 |
| SUMME |
7 |
84 |
91 |
Vierfeldertafel Nr. 6:
Vollständige Apfeldaten mit allen Daten aus der Originalquelle |
In der Vierfeldertafel Nr. 6 ist gezeigt, wie sich die Verhältnisse dann darstellen. Es ergibt sich der andere Extremfall, dass nämlich 100 % der Bio-Äpfel keine Pestizidrückstände aufweisen, wohingegen das nur bei p(konventionell sauber) = 1/84 = 1,2 % der konventionellen Äpfel der Fall ist. Auch hier muss natürlich bedacht werden, dass die Stichprobe insbesondere bei den Bio-Äpfeln nicht sehr groß ist, so dass auch 100 % nicht mit absoluter Sicherheit gleichzusetzen sind.
Übrigens weist die Studie, um die es hier ging, auch andere Daten aus, wie z.B. die verschiedenen Herkunftsländer sowie Art und Anzahl der Rückstände. Wer sich dafür interessiert, folge dem obigen Link.
Bildungs-Chancen
In einer Diskussion über Sozial- und Bildungspolitik wurde gesagt: "Im Kreis Dithmarschen kommen 70 % der Kinder, die keinen Schulabschluss schaffen, aus stationären Jugendhilfeeinrichtungen (SJHE)."
Damit sollte belegt werden, dass unser Bildungssystem Kinder aus SJHE benachteiligt. Intuitiv scheint diese Zahl, diese These auch zu unterstützen, aber wir haben ja zuvor schon gesehen, dass Wahrscheinlichkeit der Intuition oft widerspricht.
Ohne dass ich diese These bestreite, möchte ich hier darlegen, warum das vorgebrachte Argument ungültig ist. Ein falsches, irreführendes Argument erweist dem Ziel, ein wichtiges Faktum zu verbreiten, einen Bärendienst, weil es den Gegnern ermöglicht, das Faktum zu bestreiten. Deswegen ist es wichtig, auch und gerade Statistik nur entsprechend der Logik und nicht entsprechend der Intuition zu gebrauchen. Diese Webseite soll dazu beitragen, das jedem zu ermöglichen.
In diesem Fall sagen die angegebenen Zahlen nichts über Chancengleichheit aus, weil die Angaben zur Wahrscheinlichleitsverteilung fehlen:
Wie groß ist der Anteil Schüler, die keinen Abschluss machen, insgesamt?
Und wie groß ist der Anteil Schüler, die aus SJHE kommen?
Dazu später mehr.
Warum also ist das oben genannte "Argument" zur Unterstützung der These ungültig?
Es handelt sich um eine Aussage über das Ergebnis eines Zufallsexperiments (Auswahl eines Schülers aus einer Grundgesamtheit) bei der zwei Zufallsvariablen betrachtet werden:
a) Der Schüler stammt aus einer SJHE oder nicht.
b) Der Schüler hat einen Schulabschluss oder nicht.
|
Schulabschluss |
SUMME |
| JA |
NEIN |
SJHE |
JA |
a |
70 |
a + 70 |
| NEIN |
b |
30 |
b + 30 |
| SUMME |
a + b |
100 |
a + b + 100 |
| Vierfeldertafel Nr. 7
|
Wir haben oben gesehen, wie man die Wahrscheinlichkeiten in einem solchen Experiment mit Hilfe einer Vierfeldertafel berechnet.
Ich habe links eine entsprechende Vierfeldertafel (Nr. 7) dargestellt und die im "Argument" gegebene Information in die blau hinterlegten Felder eingetragen.
Im Einführungsbeispiel wurde schon gezeigt, wie wichtig die präzise Formulierung der Frage bzw. des Ereignisses ist, für das wir eine Wahrscheinlichkeit berechnen wollen.
Hier wurde die Wahrscheinlichkeit angegeben, dass ein Schüler, der keinen Schulabschluss hat, aus einer SJHE stammt.
Um die These zu unterstützen, dass unser Bildungssystem Kinder aus SJHE benachteiligt, müssen wir jedoch nach einer ganz anderen Wahrscheinlichkeit fragen:
Wie groß ist die Wahrscheinlichkeit, dass ein Schüler, der aus einer SJHE stammt, einen Schulabschluss schafft, verglichen mit der Wahrscheinlichkeit, dass ein Schüler, der nicht aus einer SJHE stammt, einen Schulabschluss macht.
Diese Wahrscheinlichkeiten lassen sich aus den gegebenen Daten nicht ermitteln!
Die Zahlen a und b, die man dafür braucht, gehören in der Vierfeldertafel zusätzlich in die roten Felder. Sie sind in dem oben genannten "Argument" aber nicht angegeben. Man kann sie aus den angegebenen Zahlen auch nicht ausrechnen!
Die Wahrscheinlichkeit, dass ein Schüler, der aus einer SJHE stammt, einen Schulabschluss (SA) schafft, beträgt p(SA | SJHE) = a / (a + 70)
Die Wahrscheinlichkeit, dass ein Schüler, der nicht aus einer SJHE stammt (SJHE), einen Schulabschluss macht, beträgt p(SA | SJHE) = b / (b + 30)
So wie in der zuerst dargestellten Anwendung der Vierfeldertafel die gesuchte Wahrscheinlichkeit dafür, bei einem positiven Test auch tatsächlich infiziert zu sein, ganz wesentlich von der Verbreitung der Krankheit sowie der Sensitivität und Spezifität des Tests abhing, so hängen die Wahrscheinlichkeiten, die wir hier vergleichen wollen, um festzustellen, ob Kinder aus SJHE in unserem Bildungssystem benachteiligt werden, davon ab, wie groß der Anteil der Kinder aus SJHE an der Gesamtzahl der Schüler ist und wie groß der Anteil der Absolventen an der Gesamtzahl der Schüler ist.
Um das zu demonstrieren, liefere ich nachstehend Beipiele, bei denen der Anteil der Kinder SJHE an den Schulabbrechern immer 70 % beträgt, bei denen aber die Wahrscheinlichkeit, einen Schulabschluss zu machen, sehr unterschiedlich sind:
Um diese Beispiele durchzurechnen, müssen wir bestimmte Annahmen treffen hinsichtlich der eben erwähnten Verhältnisse in der Grundgesamtheit bezüglich der beiden Variablen a und b. (Auch andere Angaben, die die Berechnung dieser Werte aus den Summenzellen erlauben, sind möglich.)
Mit anderen Worten: Um die gesuchten Wahrscheinlichkeiten zu berechnen, müssen wir eine Wahrscheinlichkeitsverteilung zu Grunde legen!
Dazu nehme ich in den jeweiligen Beispielen bestimmte Werte an, die jeweils im Text und unter der zugehörigen Vierfeldertafel genannt sind.
|
Schulabschluss |
SUMME |
| JA |
NEIN |
SJHE |
JA |
30 |
70 |
100 |
| NEIN |
9.870 |
30 |
9.900 |
| SUMME |
9.900 |
100 |
10.000 |
Vierfeldertafel Nr. 8:
1 % ohne Schulabschluss
1 % Schüler aus SJHE
|
Das erste Beispiel habe ich in Vierfeldertafel Nr. 8 dargestellt: Die angenommene Wahrscheinlichkeitsverteilung ist, dass 1 % der Schüler kein Abschlusszeugnis erhalten und dass der Anteil der Kinder aus stationären Jugendhilfeeinrichtungen an der Gesamtzahl der Schüler ebenfalls 1 % beträgt.
In dieser Konstellation berechnen sich die gesuchten Wahrscheinlichkeiten zu:
Die Wahrscheinlichkeit, dass ein Schüler, der aus einer SJHE stammt, einen Schulabschluss (SA) schafft, beträgt p(SA | SJHE) = 30 / 100 = 30 %
Die Wahrscheinlichkeit, dass ein Schüler, der nicht aus einer SJHE stammt (SJHE), einen Schulabschluss macht, beträgt p(SA | SJHE) = 9.870 / 9.900 = 99,7 %
In dieser Konstellation ergibt sich also ein Ergebnis, das demjenigen gleicht, das auch durch die in der Diskussion angegebenen Zahlen suggeriert wird.
Das ist immer so, wenn die beiden Anteile für Schüler ohne Abschluss und für Schüler aus SJHE gleich sind.
Allerdings wird dabei die Chance auf einen Schulabschluss kleiner für Schüler, die nicht aus einer SJHE stammen, wenn der Anteil der Schulabbrecher insgesamt steigt.
In der Vierfeldertafel mit Eingabemöglichkeiten kann man das ausprobieren, indem man z.B. p(SJHE) = 10 % und p(SA) = 90 % eingibt.
|
Schulabschluss |
SUMME |
| JA |
NEIN |
SJHE |
JA |
1.930 |
70 |
2.000 |
| NEIN |
7.970 |
30 |
8.000 |
| SUMME |
9.900 |
100 |
10.000 |
Vierfeldertafel Nr. 9:
1 % ohne Schulabschluss
20 % Schüler aus SJHE
|
In der Vierfeldertafel Nr. 9 habe ich angenommen, dass 1 % der Schüler keinen Abschluss machen und dass 20 % der Schüler aus stationären Jugendhilfeeinrichtungen stammen. Bei dieser Wahrscheinlichkeitsverteilung ergibt sich ein völlig anderes Bild:
Die Wahrscheinlichkeit, dass ein Schüler, der aus einer SJHE stammt, einen Schulabschluss (SA) schafft, beträgt p(SA | SJHE) = 1.930 / 2.000 = 96,5 %
Die Wahrscheinlichkeit, dass ein Schüler, der nicht aus einer SJHE stammt (SJHE), einen Schulabschluss macht, beträgt p(SA | SJHE) = 7.970 / 8.000 = 99,6 %
In diesem Fall besteht also kein signifikanter Unterschied mehr zwischen den Chancen auf einen Schulabschluss.
|
Schulabschluss |
SUMME |
| JA |
NEIN |
SJHE |
JA |
7.430 |
70 |
7.500 |
| NEIN |
2.470 |
30 |
2.500 |
| SUMME |
9.900 |
100 |
10.000 |
Vierfeldertafel Nr. 10:
1 % ohne Schulabschluss
75 % Schüler aus SJHE
|
In nebenstehender Vierfeldertafel Nr. 10 ist eine Konstellation gezeigt, bei der die Chance der Schüler aus SJHE, einen Schulabschluss zu erreichen, sogar größer ist, als die der anderen. Mit anderen Worten: Das zu Beginn des Kapitels angeführte "Argument" könnte bei intuitiver Schlussfolgerung sogar eine falsche These stützen!
Die Abbrecherquote ist hier mit 1 % und der Anteil der Schüler aus SJHE mit 75 % angesetzt.
Die Wahrscheinlichkeit, dass ein Schüler, der aus einer SJHE stammt, einen Schulabschluss (SA) schafft, beträgt dann p(SA | SJHE) = 7.430 / 7.500 = 99,1 %
Die Wahrscheinlichkeit, dass ein Schüler, der nicht aus einer SJHE stammt (SJHE), einen Schulabschluss macht, beträgt dagegen p(SA | SJHE) = 2.470 / 2.500 = 98,8 %, ist also kleiner.
Zusammenfassend lässt sich sagen, dass immer dann wenn der Anteil Schüler aus stationären Jugendhilfeeinrichtungen größer ist als der Anteil an Schülern, die keinen Schulabschluss erreichen (in VFT Nr. 9: 20 % > 1 %), die Chance einen Schulabschluss zu erreichen für diese Schüler größer ist als die durch das falsche "Argument" suggerierten 30 %.
Schüler aus SJHE haben eine kleinere Chance als die anderen, solange ihr Anteil an der Zahl der Schüler kleiner ist als ihr Anteil an der Zahl der Schulabbrecher (in VFT Nr. 9: 20 % < 70 %).
Ist ihr Anteil größer, kehrt sich der Chancenvergleich sogar um (VFT Nr. 10: 75 % > 70 %)! Im Extremfall ist das falsche "Argument" also sogar eingesetzt worden, um eine falsche These zu belegen.
Auch wenn - oder gerade weil! - ich der Meinung bin, dass sich die Chancengleichheit in unserem Bildungssystem noch deutlich verbessern muss, halte ich es für unseriös und kontraproduktiv, das eingangs dargestellte "Argument" in der Diskussion um Möglichkeiten und Wege zur Verbesserung der Chancengleichheit einzusetzen!
Ohne die Angabe der Wahrscheinlichkeitsverteilung sagt dieses "Argument" genau nichts aus!
Vermutlich werden diese Zahlen sogar im guten Glauben, sie seien ein schlagkräftiges Argument, benutzt. Das wiederum ist Ausdruck der Tatsache, dass unser Bildungssystem auch und besonders im Bereich Mathematik verbessert werden muss - und zwar für alle!
Wie sind nun die realen Verhältnisse?
Ich habe an das Statistikamt Nord geschrieben und um entsprechende Auskunft gebeten.
Folgendes hat man mir umgehend geantwortet:
Im Jahr 2020 gab es im Kreis Dithmarschen 134 junge Menschen, die in Heimerziehung oder einer sonstigen betreuten Wohnform waren, darunter 111 im Alter von 6 bis unter 18 Jahren.
Die Gesamtzahl der Schüler im Schuljahr 2020/21 betrug 12.772 und die Anzahl der mit Schulabschluss Entlassenen betrug 1.225.
Aus dem Kreismonitor des Statistikamtes Nord kann man entnehmen, dass im Jahr 2020 in Dithmarschen 10,2 % der Schüler die Schule ohne Abschluss verlassen haben. Also ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Schüler einen Schulabschluss erreicht p(SA) = 89,8 %. (Meiner Meinung nach auch ein Armutszeugnis für unser Bildungssystem! Mehr als jeder Zehnte hat keinen Schulabschluss!!)
|
Schulabschluss |
SUMME |
| JA |
NEIN |
SJHE |
JA |
37 |
97 |
134 |
| NEIN |
1.188 |
42 |
1.230 |
| SUMME |
1.225 |
139 |
1.364 |
Vierfeldertafel Nr. 11:
Aus verschiedenen Statistiken zusammengestellte Daten
|
Mit diesen Angaben habe ich nebenstehende Vierfeldertafel Nr. 11 wie folgt zusammengestellt:
Aus der gegebenen Anzahl von 1.225 Absolventen und der Abbrecherquote lässt sich die Gesamtzahl der Schüler in Abschlussklassen berechnen:
1.225 / (1 − 0,102) = 1.364
Aus der Differenz dieser beiden Zahlen ergibt sich die Gesamtzahl der Schüler ohne Abschluss zu 139.
Wendet man das im anfangs erwähnten "Argument" genannte Verhältnis 70/30 auf die Zahl der Schüler ohne Abschluss an und rundet auf ganze Personenzahlen, erhält man 139 x 0,7 = 97 und 139 x 0,3 = 42 für die Aufteilung der Schüler ohne Abschluss auf die Herkunft aus SJHE bzw. nicht aus SJHE.
Die Differenz aus Schülergesamtzahl und Anzahl Schüler aus SJHE ergibt die Zahl der Schüler, die nicht in SJHE leben.
Damit ist die Vierfeldertafel komplett und wir können die uns interessierenden Wahrscheinlichkeiten ausrechenen:
Die Wahrscheinlichkeit, dass ein Schüler, der aus einer SJHE stammt, einen Schulabschluss (SA) schafft, beträgt dann p(SA | SJHE) = 37 / 134 = 27,6 %
Die Wahrscheinlichkeit, dass ein Schüler, der nicht aus einer SJHE stammt (SJHE), einen Schulabschluss macht, beträgt dagegen p(SA | SJHE) = 1.188 / 1.230 = 96,6 %.
Man kann also konstatieren, dass die intuitive aber falsche Schlussfolgerung aus dem Eingangs-"Argument" zum richtigen Ergebnis führt.
Wie oben gezeigt ist dies jedoch keineswegs selbstverständlich sondern es können auch ganz andere Sachverhalte zu den gegebenen Zahlen führen und damit eine falsche These "belegen".
Nachstehende Vierfeldertafel mit Eingabemöglichkeiten gibt Ihnen die Gelegenheit, ein wenig zu experimentieren: Die beiden Ereignisse, die betrachtet werden, sind jetzt weder Äpfel aus biologischem Anbau noch Schüler aus stationären Jugendhilfeeinrichtungen sondern nur noch A und B.
Geben Sie in das Eingabefeld p(A) den Anteil derjenigen Zufallsexperimente an allen Experimenten ein, die das Ergebnis A haben!
Geben Sie in das Eingabefeld p(B) den Anteil derjenigen Zufallsexperimente an allen Experimenten ein, die das Ergebnis B haben!
Und geben Sie zuguterletzt in das Eingabefeld p(B|A) den Anteil derjenigen Zufallsexperimente an denen mit Ergbnis B ein, die das Ergebnis A haben!
Die Felder der Tafel werden dann automatisch berechnet und die bedingten Wahrscheinlichkeiten p(A | B) und p(A | B) angegeben.
Man kann das oben Gesagte auch wie folgt zusammenfassen: "Vernunft bedeutet nicht, Fakten zu kennen, sondern zu wissen, welche Fakten relevant sind."
Das ist auf dem Youtube-Kanal 3Blue1Brown von Grant Sanderson (in englischer Sprache)
ganz hervorragend beschrieben, außerdem
wie man den Einfluss der Randbedingungen schneller als mit einer Vierfeldertafel überschlagsmäßigberücksichtigen kann.
Sehr empfehlenswert ist auch das Buch "Thinking Fast and Slow" von Daniel Kahnemann, das es auch in deutscher Übersetzung gibt. Darin sind noch mehr Phänomene beschrieben, bei denen unsere Intuition uns ähnlich in die Irre führt wie bei den hier beschriebenen Beispielen.
Bei Veritasium auf YouTube gibt es auch ein empfehlenswertes Video (in Englisch), das sich mit der Problematik der Interpretation statistischer Daten befasst!
Wie wichtig es ist, immer ganz genau hinzuschauen, was eine Statistik eigentlich aussagt und worauf sich angegebene Prozentwerte beziehen, stellt Correctiv in seinem Artikel Faktencheck zum Bürgergeld: Grafik zu Bezügen von Geflüchteten ist irreführend sehr eindrucksvoll und sachlich dar!
 Ausgehend von einem Startpunkt (links im Bild) zeichnet man einen Pfeil zu jedem möglichen Ergebnis des ersten Teilexperiments. In unserem Beispiel gibt es die drei Möglichkeiten, eine rote, eine gelbe oder eine blaue Kugel zu ziehen.
Ausgehend von einem Startpunkt (links im Bild) zeichnet man einen Pfeil zu jedem möglichen Ergebnis des ersten Teilexperiments. In unserem Beispiel gibt es die drei Möglichkeiten, eine rote, eine gelbe oder eine blaue Kugel zu ziehen.
 Ein Promille der Menschen leide an einer Krankheit, die erst einige Zeit nach der Infektion ausbreche und dann schwere Folgen habe. Sie sei nur heilbar, wenn sie vor dem Ausbruch diagnostiziert werde. Während der Inkubationszeit (der Zeit zwischen Infektion und Ausbruch) sei sie ohne Symptome und könne nur mit einem Test festgestellt werden. Dieser Test habe eine Sensitivität von 97 %. Das bedeutet, dass der Test in 97 % der Fälle bei einer tatsächlich infizierten Person ein positives Ergebnis liefert. Mit einer gewissen Wahrscheinlichkeit - in diesem Beispiel wollen wir 2 % annehmen - liefere der Test aber auch dann ein positives Ergebnis, wenn die getestete Person nicht infiziert ist. Man könnte das die Falschalarmrate nennen, Mediziner sprechen statt dessen aber lieber von einer Spezifität von 98 %.
Ein Promille der Menschen leide an einer Krankheit, die erst einige Zeit nach der Infektion ausbreche und dann schwere Folgen habe. Sie sei nur heilbar, wenn sie vor dem Ausbruch diagnostiziert werde. Während der Inkubationszeit (der Zeit zwischen Infektion und Ausbruch) sei sie ohne Symptome und könne nur mit einem Test festgestellt werden. Dieser Test habe eine Sensitivität von 97 %. Das bedeutet, dass der Test in 97 % der Fälle bei einer tatsächlich infizierten Person ein positives Ergebnis liefert. Mit einer gewissen Wahrscheinlichkeit - in diesem Beispiel wollen wir 2 % annehmen - liefere der Test aber auch dann ein positives Ergebnis, wenn die getestete Person nicht infiziert ist. Man könnte das die Falschalarmrate nennen, Mediziner sprechen statt dessen aber lieber von einer Spezifität von 98 %.
